문제 >
드래곤 커브는 다음과 같은 세 가지 속성으로 이루어져 있으며, 이차원 좌표 평면 위에서 정의된다. 좌표 평면의 x축은 → 방향, y축은 ↓ 방향이다.
- 시작 점
- 시작 방향
- 세대
0세대 드래곤 커브는 아래 그림과 같은 길이가 1인 선분이다. 아래 그림은 (0, 0)에서 시작하고, 시작 방향은 오른쪽인 0세대 드래곤 커브이다.

1세대 드래곤 커브는 0세대 드래곤 커브를 끝 점을 기준으로 시계 방향으로 90도 회전시킨 다음 0세대 드래곤 커브의 끝 점에 붙인 것이다. 끝 점이란 시작 점에서 선분을 타고 이동했을 때, 가장 먼 거리에 있는 점을 의미한다.

2세대 드래곤 커브도 1세대를 만든 방법을 이용해서 만들 수 있다. (파란색 선분은 새로 추가된 선분을 나타낸다)

3세대 드래곤 커브도 2세대 드래곤 커브를 이용해 만들 수 있다. 아래 그림은 3세대 드래곤 커브이다.
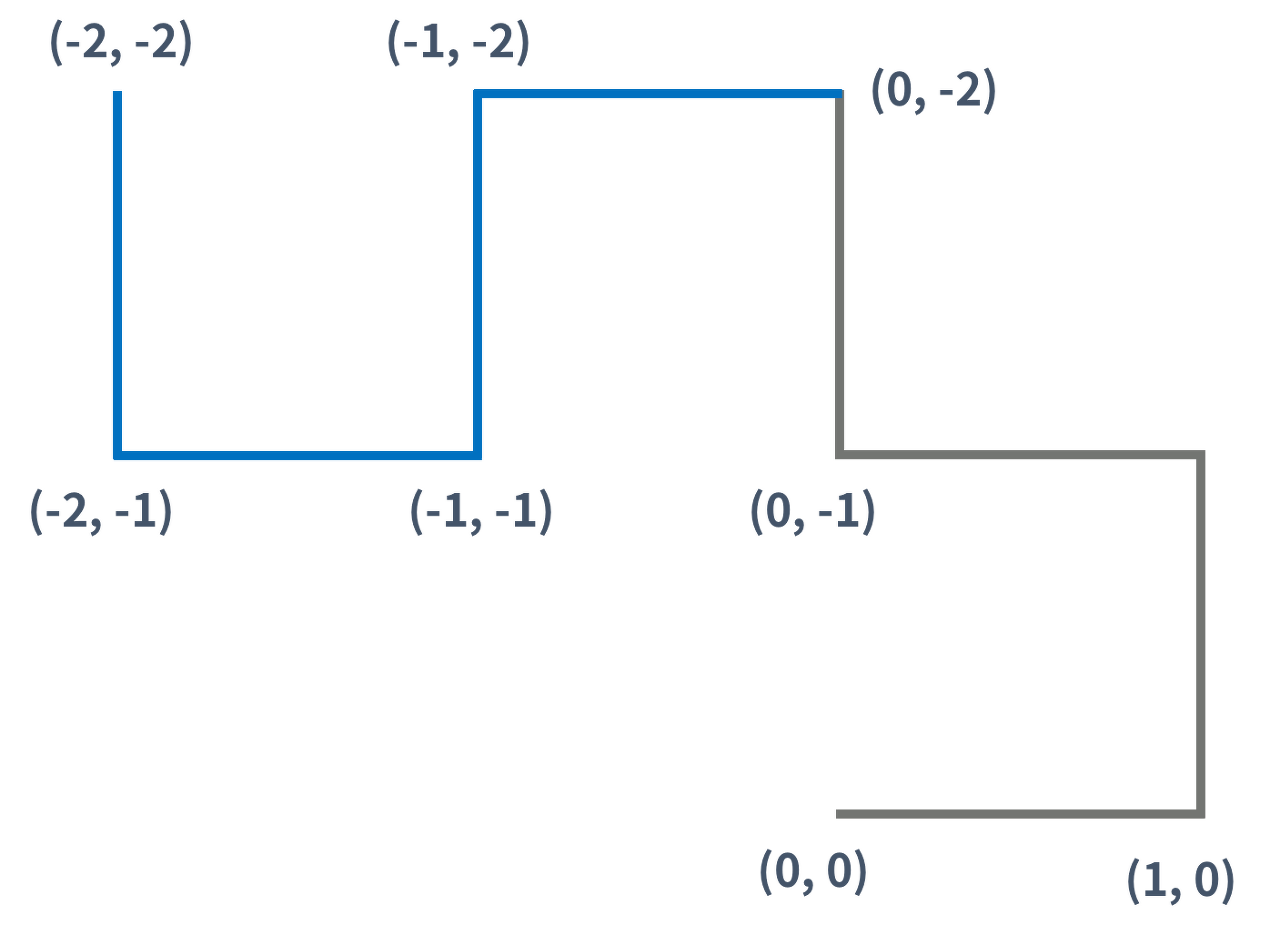
즉, K(K > 1)세대 드래곤 커브는 K-1세대 드래곤 커브를 끝 점을 기준으로 90도 시계 방향 회전 시킨 다음, 그것을 끝 점에 붙인 것이다.
크기가 100×100인 격자 위에 드래곤 커브가 N개 있다. 이때, 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 정사각형의 개수를 구하는 프로그램을 작성하시오. 격자의 좌표는 (x, y)로 나타내며, 0 ≤ x ≤ 100, 0 ≤ y ≤ 100만 유효한 좌표이다.
입력 >
첫째 줄에 드래곤 커브의 개수 N(1 ≤ N ≤ 20)이 주어진다. 둘째 줄부터 N개의 줄에는 드래곤 커브의 정보가 주어진다. 드래곤 커브의 정보는 네 정수 x, y, d, g로 이루어져 있다. x와 y는 드래곤 커브의 시작 점, d는 시작 방향, g는 세대이다. (0 ≤ x, y ≤ 100, 0 ≤ d ≤ 3, 0 ≤ g ≤ 10)
입력으로 주어지는 드래곤 커브는 격자 밖으로 벗어나지 않는다. 드래곤 커브는 서로 겹칠 수 있다.
방향은 0, 1, 2, 3 중 하나이고, 다음을 의미한다.
- 0: x좌표가 증가하는 방향 (→)
- 1: y좌표가 감소하는 방향 (↑)
- 2: x좌표가 감소하는 방향 (←)
- 3: y좌표가 증가하는 방향 (↓)
출력 >
첫째 줄에 크기가 1×1인 정사각형의 네 꼭짓점이 모두 드래곤 커브의 일부인 것의 개수를 출력한다.
해결방법 >
두 가지 방법으로 해결해봤다.
1) 첫 번째는 좌표를 모두 직접 찍어보는 방법이다.
드래곤 커브는 한 세대를 거칠 때마다 끝점을 기준으로 대칭성을 보인다.
문제에서 나온 4세대를 기준으로 보면 각 좌표는 아래와 같다.(빨간색으로 표시된 좌표는 이전 세대에서 끝점이다)
좌표 : (0, 0) (1, 0) (1, -1) (0, -1) (0, -2) (-1, -2) (-1, -1) (-2, -1) (-2, -2)
\ / \ / \ / \ / \ / \ / \ / \ /
차이 : (1, 0) (0, -1) (-1, 0) (0, -1) (1, 0) (0, 1) (-1, 0) (0, -1)
3세대의 끝점을 p[i]라고 하면 (0, -2)
p[i+1] = p[i] + (1, 0)
p[i-1] = p[i] - (0, -1)
좌표 : (0, 0) (1, 0) (1, -1) (0, -1) (0, -2) (-1, -2) (-1, -1) (-2, -1) (-2, -2)
\ / \ / \ / \ / \ / \ / \ / \ /
차이 : (1, 0) (0, -1) (-1, 0) (0, -1) (1, 0) (0, 1) (-1, 0) (0, -1)
p[i+2] = p[i+1] + (0, 1)
p[i-2] = p[i-1] - (-1, 0)
좌표 : (0, 0) (1, 0) (1, -1) (0, -1) (0, -2) (-1, -2) (-1, -1) (-2, -1) (-2, -2)
\ / \ / \ / \ / \ / \ / \ / \ /
차이 : (1, 0) (0, -1) (-1, 0) (0, -1) (1, 0) (0, 1) (-1, 0) (0, -1)
p[i+3] = p[i+2] + (-1, 0)
p[i-3] = p[i-2] - (0, -1)
좌표 : (0, 0) (1, 0) (1, -1) (0, -1) (0, -2) (-1, -2) (-1, -1) (-2, -1) (-2, -2)
\ / \ / \ / \ / \ / \ / \ / \ /
차이 : (1, 0) (0, -1) (-1, 0) (0, -1) (1, 0) (0, 1) (-1, 0) (0, -1)
위와 같은 방식으로 대칭성을 찾아보면 아래와 같다.
fp gp
(0, -1) -> (1, 0)
(-1, 0) -> (0, 1)
(0, -1) -> (-1, 0)
(1, 0) -> (0, -1)
즉, p[n]을 이전 세대의 끝점이라고 한다면
p[n-i] = p[n-i-1] - fp를 통해
p[n+i] = p[n+i-1] + gp를 구할 수 있다.
한마리도 끝점을 기준으로 이전 좌표를 통해 다음 좌표를 구할 수 있다.
2) 두 번째 좌표는 방향만으로 좌표를 모두 찾는 것이다.
문제에 나온 예시를 들어보면
1세대일 때 방향은 0
2세대일 때 방향은 0, 1
3세대일 때 방향은 0, 1, 2, 1
4세대일 때 방향은 0, 1, 2, 1, 2, 3, 2, 1이다
i세대일 때 방향은 (i-1)세대일 때 방향에 모두 1씩 증가시켜준 값이다.
따라서 i세대까지의 모든 방향을 구하고 방향에 따라 좌표를 찾는다.
[JAVA]
package baekjoon;
import java.util.*;
public class s_15685 {
static int[][] map;
static int cnt;
public static class Node{
int x;
int y;
Node(int x, int y){
this.x = x;
this.y = y;
}
}
public static Node go(int x, int y) {
Node next;
if(x == 1 && y == 0) next = new Node(0, -1);
else if(x == -1 && y == 0) next = new Node(0, 1);
else if(x == 0 && y == -1) next = new Node(-1, 0);
else next = new Node(1, 0);
return next;
}
public static void dragon(int x, int y, int[] d, int period) {
ArrayList<Node> a = new ArrayList<>();
ArrayList<Node> dp = new ArrayList<>();
a.add(new Node(x, y));
x = x + d[0];
y = y + d[1];
a.add(new Node(x, y));
dp.add(new Node(a.get(1).x - a.get(0).x, a.get(1).y - a.get(0).y));
for(int i = 0; i < period; i++) {
int dp_size = dp.size();
for(int j = 0; j < dp_size; j++) {
int tmpx = dp.get(dp_size - 1 - j).x;
int tmpy = dp.get(dp_size - 1 - j).y;
Node node = go(tmpx, tmpy);
int nx = a.get(a.size()-1).x + node.x;
int ny = a.get(a.size()-1).y + node.y;
a.add(new Node(nx, ny));
dp.add(new Node(node.x, node.y));
}
}
for(int i = 0; i < a.size(); i++) {
if(a.get(i).x >= 0 && a.get(i).y >= 0 && a.get(i).x <= 100 && a.get(i).y <= 100){
map[a.get(i).x][a.get(i).y] = 1;
}
}
}
public static void count() {
for(int i = 0; i <= 100; i++) {
for(int j = 0; j <= 100; j++) {
if(map[i][j] == 1) {
if(i+1 <= 100 && j+1 <= 100) {
if(map[i+1][j] == 1 && map[i][j+1] == 1 && map[i+1][j+1] == 1) cnt++;
}
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int[][] direct = {{1,0}, {0, -1}, {-1, 0}, {0, 1}};
map = new int[101][101];
int n = sc.nextInt();
for(int i = 0; i < n; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int d = sc.nextInt();
int p = sc.nextInt();
dragon(x, y, direct[d], p);
}
count();
System.out.println(cnt);
}
}
package baekjoon;
import java.util.*;
public class s_15685_2 {
static int[] dx = {1, 0, -1, 0};
static int[] dy = {0, -1, 0, 1};
static int[][] map;
static int cnt;
public static void go(int x, int y, int d, int p) {
ArrayList <Integer> a = new ArrayList<>();
map[x][y] = 1;
a.add(d);
for(int i = 0; i < p; i++) {
int size = a.size();
for(int j = 0; j < size; j++) {
d = a.get(size - 1 - j) + 1;
if(d > 3) d = 0;
a.add(d);
}
}
for(int i = 0; i < a.size(); i++) {
x += dx[a.get(i)];
y += dy[a.get(i)];
map[x][y] = 1;
}
}
public static void count() {
for(int i = 0; i < 100; i++) {
for(int j = 0; j < 100; j++) {
if(map[i][j] == 1 && map[i+1][j] == 1 && map[i][j+1] == 1 && map[i+1][j+1] == 1) cnt++;
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
map = new int[101][101];
cnt = 0;
for(int i = 0; i < n; i++) {
int x = sc.nextInt();
int y = sc.nextInt();
int d = sc.nextInt();
int p = sc.nextInt();
go(x, y, d, p);
}
count();
System.out.println(cnt);
}
}
'Problem Solving > BOJ' 카테고리의 다른 글
| [백준] 14888번 - 연산자 끼워넣기 (0) | 2020.03.14 |
|---|---|
| [백준] 14501번 - 퇴사 (0) | 2020.03.14 |
| [백준] 14889번 - 스타트와 링크 (0) | 2020.03.13 |
| [백준] 14503번 - 로봇 청소기 (0) | 2020.03.13 |
| [백준] 14890번 - 경사로 (0) | 2020.03.12 |


댓글