문제 >
재현시의 시장 구재현은 지난 몇 년간 게리맨더링을 통해서 자신의 당에게 유리하게 선거구를 획정했다. 견제할 권력이 없어진 구재현은 권력을 매우 부당하게 행사했고, 심지어는 시의 이름도 재현시로 변경했다. 이번 선거에서는 최대한 공평하게 선거구를 획정하려고 한다.
재현시는 크기가 N×N인 격자로 나타낼 수 있다. 격자의 각 칸은 구역을 의미하고, r행 c열에 있는 구역은 (r, c)로 나타낼 수 있다. 구역을 다섯 개의 선거구로 나눠야 하고, 각 구역은 다섯 선거구 중 하나에 포함되어야 한다. 선거구는 구역을 적어도 하나 포함해야 하고, 한 선거구에 포함되어 있는 구역은 모두 연결되어 있어야 한다. 구역 A에서 인접한 구역을 통해서 구역 B로 갈 수 있을 때, 두 구역은 연결되어 있다고 한다. 중간에 통하는 인접한 구역은 0개 이상이어야 하고, 모두 같은 선거구에 포함된 구역이어야 한다.
선거구를 나누는 방법은 다음과 같다.
- 기준점 (x, y)와 경계의 길이 d1, d2를 정한다. (d1, d2 ≥ 1, 1 ≤ x < x+d1+d2 ≤ N, 1 ≤ y-d1 < y < y+d2 ≤ N)
- 다음 칸은 경계선이다.
- (x, y), (x+1, y-1), ..., (x+d1, y-d1)
- (x, y), (x+1, y+1), ..., (x+d2, y+d2)
- (x+d1, y-d1), (x+d1+1, y-d1+1), ... (x+d1+d2, y-d1+d2)
- (x+d2, y+d2), (x+d2+1, y+d2-1), ..., (x+d2+d1, y+d2-d1)
- 경계선과 경계선의 안에 포함되어있는 5번 선거구이다.
- 5번 선거구에 포함되지 않은 구역 (r, c)의 선거구 번호는 다음 기준을 따른다.
- 1번 선거구: 1 ≤ r < x+d1, 1 ≤ c ≤ y
- 2번 선거구: 1 ≤ r ≤ x+d2, y < c ≤ N
- 3번 선거구: x+d1 ≤ r ≤ N, 1 ≤ c < y-d1+d2
- 4번 선거구: x+d2 < r ≤ N, y-d1+d2 ≤ c ≤ N
아래는 크기가 7×7인 재현시를 다섯 개의 선거구로 나눈 방법의 예시이다.

구역 (r, c)의 인구는 A[r][c]이고, 선거구의 인구는 선거구에 포함된 구역의 인구를 모두 합한 값이다. 선거구를 나누는 방법 중에서, 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 구해보자.
입력 >
첫째 줄에 재현시의 크기 N이 주어진다.
둘째 줄부터 N개의 줄에 N개의 정수가 주어진다. r행 c열의 정수는 A[r][c]를 의미한다.
출력 >
첫째 줄에 인구가 가장 많은 선거구와 가장 적은 선거구의 인구 차이의 최솟값을 출력한다.
해결방법 >
항상 많은 것을 배울 수 있게 해주는 친구가 SW역량테스트에서 풀었던 문제다.
그래서 좀더 흥미를 가지고 풀 수 있었던 문제였다.
문제는 다음과 같은 과정을 거친다.
1) 경계선을 만든다.
2) BFS로 경계선을 기준으로 선거구 번호를 매긴다.
3) 인원수를 구한다.
n = 4일 때 선거구역을 나누는 예를 들어보자
1) 경계선을 만든다.
경계선을 만드는 조건은 (d1, d2 ≥ 1, 1 ≤ y < y+d1+d2 ≤ N, 1 ≤ x-d1 < x < x+d2 ≤ N)이므로
조건을 만족하는 x, y, d1, d2를 경우를 찾는다. (편의상 문제의 보여준 x,y를 바꿔줌)
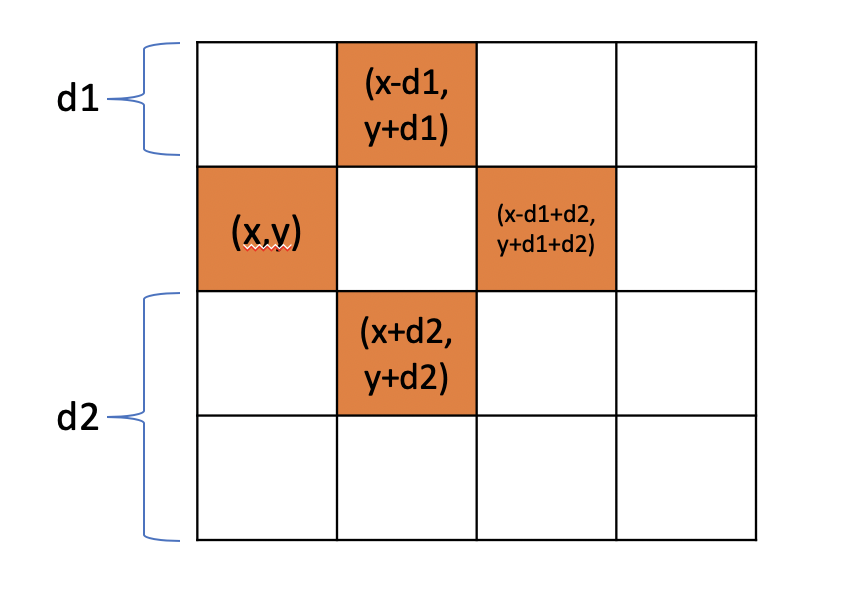
2) 경계선을 만들었다면 BFS로 각 선거구의 번호를 정점마다 매겨준다.
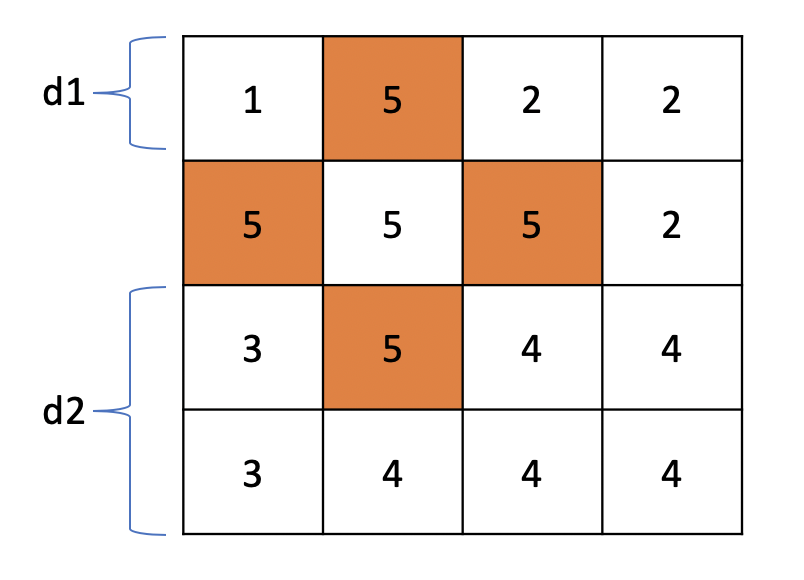
3) 선거구의 번호를 기준으로 입력받았던 이차원 배열과 비교해 각 선거구마다 인구수를 합해준다.
선거구를 나눌 때마다 가장 큰 인원과 작은 인원의 차를 구하고 이 중 최솟값을 출력한다.
[JAVA]
package baekjoon;
import java.util.*;
public class BOJ_17779 {
static int[][] map;
static int n;
static int[][] a;
static int diff;
public static void cal() {
int[] vote = new int[5];
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
vote[map[i][j] - 1] += a[i][j];
}
}
int max = vote[0];
int min = vote[0];
for(int i = 1; i < 5; i++) {
min = Math.min(min, vote[i]);
max = Math.max(max, vote[i]);
}
diff = Math.min(diff, max - min);
}
public static class Node{
int x;
int y;
Node(int x, int y){
this.x = x;
this.y = y;
}
}
public static void bfs(int x, int y, int v) {
Queue <Node> q = new LinkedList<>();
int[] dx = {-1, 0, 1, 0};
int[] dy = {0, 1, 0, -1};
q.add(new Node(x, y));
map[x][y] = v;
while(!q.isEmpty()) {
Node node = q.poll();
x = node.x;
y = node.y;
for(int i = 0; i < 4; i++) {
int nx = x + dx[i];
int ny = y + dy[i];
if(nx >= 0 && ny >= 0 && nx < n && ny < n && map[nx][ny] == 0) {
map[nx][ny] = v;
q.add(new Node(nx, ny));
}
}
}
}
public static void part(int x, int y, int d1, int d2) {
draw(x, y, -1, 1, d1);
draw(x-d1, y+d1, 1, 1, d2);
draw(x-d1+d2, y+d1+d2, 1, -1, d1);
draw(x+d2, y+d2, -1, -1, d2);
for(int i = 0; i < x-d1; i++) {
map[i][y+d1] = 1;
}
for(int i = y+d1+d2+1; i < n; i++) {
map[x-d1+d2][i] = 2;
}
for(int i = 0; i < y; i++) {
map[x][i] = 3;
}
for(int i = x+d2+1; i < n; i++) {
map[i][y+d2] = 4;
}
bfs(0, 0, 1);
bfs(0, n-1, 2);
bfs(n-1, 0, 3);
bfs(n-1, n-1, 4);
bfs(x, y, 5);
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
if(map[i][j] == 0) map[i][j] = 5;
}
}
}
public static void draw(int x, int y, int dx, int dy, int depth) {
if(depth == 0) return;
map[x][y] = 5;
draw(x+dx, y+dy, dx, dy, depth-1);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
a = new int[n][n];
diff = 9999999;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
a[i][j] = sc.nextInt();
}
}
for(int i = 1; i < n; i++) {
for(int j = 0; j < n - 2; j++) {
for(int l = 1; l <= i; l++) {
for(int k = 1; k < n - i; k++) {
if(j + l + k < n) {
map = new int[n][n];
part(i, j, l, k);
cal();
}
}
}
}
}
System.out.println(diff);
}
}
'Problem Solving > BOJ' 카테고리의 다른 글
| [백준] 17140번 - 이차원 배열과 연산 (0) | 2020.03.15 |
|---|---|
| [백준] 15686번 - 치킨 배달 (0) | 2020.03.14 |
| [백준] 14891번 - 톱니바퀴 (0) | 2020.03.14 |
| [백준] 14888번 - 연산자 끼워넣기 (0) | 2020.03.14 |
| [백준] 14501번 - 퇴사 (0) | 2020.03.14 |

댓글