Autoencoder
1. 오토인코더(Autoencoder)
어떤 지도 없이 잠재표현(latent representation) 또는 코딩(coding)이라 부르는 input data의 밀집 표현을 학습할 수 있는 인공 신경망
코딩은 input data 보다 훨씬 낮은 차원을 가지므로 차원 축소(dimenssion reduction), 시각화 등에 사용되고,
강력한 특성 추출기(Feature Exractor)처럼 동작하기 떄문에 심층 신경망의 비지도 사전 훈련에 사용.
또한, 일부 오토 인코더는 훈련 데이터와 매우 비슷한 새로운 데이터를 생성하는 생성 모델(generative model)로도 활용될 수 있다.
오토 인코더는 단순히 입력을 출력으로 복사하는 방법을 배우는데,
latent space의 크기를 제한하거나 input에 noise를 추가해 원본을 복원하도록 네트워크를 훈련하는 등을 제약을 통해 오토 인코더가 입력을 출력으로 바로 복사하지 못하도록 막고 효율적으로 표현하는 방법을 만든다.
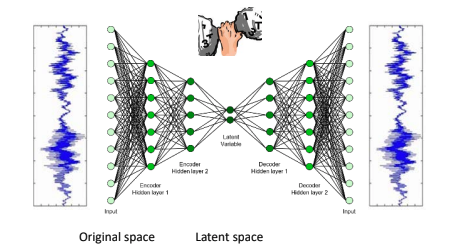
오토 인코더는 두 부분으로 구성된다.
입력 데이터를 내부 표현으로 압축하는 인코더(Encoder 또는 Recognition network)와
내부 표현을 원본 데이터로 복원하는 디코더(Decoder 또는 generative network)이다.
오토 인코더는 입력층과 출력 층의 뉴런 개수가 동일한 것을 제외하면 MLP와 동일한 구조를 가진다.
오토 인코더는 입력을 재구성하기 때문에 출력은 재구성(Reconstruction)이라고 부른다.
비용 함수는 Reconstruction과 input의 차이(Reconstruction loss)를 포함한다.
오토 인코더는 input을 dimession reduction을 통해 저차원의 latent space를 만들기 때문에 이러한 오토 인코더를 undercomplete autoencoder라 한다.
PCA와 autoencoder 차이
PCA는 활성화 함수로 선형 함수를 사용하고, autoencoder는 주로 시그모이드 함수와 같은 비선형 함수를 사용한다.
autoencoder에서 dense layer를 형성할 때, 활성화 함수를 선형 함수로 구성한다면 PCA와 (이론적으론) 똑같은 결과를 만든다.
Undercomplete autoencoder로 PCA 구현하기
np.random.seed(4)
def generate_3d_data(m, w1=0.1, w2=0.3, noise=0.1):
angles = np.random.rand(m) * 3 * np.pi / 2 - 0.5
data = np.empty((m, 3))
data[:, 0] = np.cos(angles) + np.sin(angles)/2 + noise * np.random.randn(m) / 2
data[:, 1] = np.sin(angles) * 0.7 + noise * np.random.randn(m) / 2
data[:, 2] = data[:, 0] * w1 + data[:, 1] * w2 + noise * np.random.randn(m)
return data
X_train = generate_3d_data(60)
X_train = X_train - X_train.mean(axis=0, keepdims=0)
encoder = keras.models.Sequential([keras.layers.Dense(2, input_shape=[3])])
decoder = keras.models.Sequential([keras.layers.Dense(3, input_shape=[2])])
autoencoder = keras.models.Sequential([encoder, decoder])
autoencoder.compile(loss="mse", optimizer=keras.optimizers.SGD(learning_rate=1.5))
autoencoder.fit(X_train, X_train, epochs=20)
codings = encoder.predict(X_train)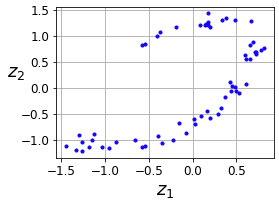
Stacked autoencoder
은닉층을 여러개 가지는 autoencoder를 stacked autoencoder 또는 deep autoencoder라 하며,
은닉층을 여러개 쌓을수록 오토 인코더는 더 정교한 coding을 만들어내지만,
general한 model을 만들어내지 못할 수 있으므로 주의해야한다.
stacked autoencoder는 latent space를 기준으로 대칭적인 구조를 이루며, 마찬가지로 입력층과 출력층의 노드 개수는 같다

케라스로 구현한 Deep autoencoder
(X_train_full, y_train_full), (X_test, y_test) = keras.datasets.fashion_mnist.load_data()
X_train_full = X_train_full.astype(np.float32) / 255
X_test = X_test.astype(np.float32) / 255
X_train, X_valid = X_train_full[:-5000], X_train_full[-5000:]
y_train, y_valid = y_train_full[:-5000], y_train_full[-5000:]
tf.random.set_seed(42)
np.random.seed(42)
stacked_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation="selu"),
keras.layers.Dense(30, activation="selu"),
])
stacked_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation="selu", input_shape=[30]),
keras.layers.Dense(28 * 28, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
stacked_ae = keras.models.Sequential([stacked_encoder, stacked_decoder])
stacked_ae.compile(loss="binary_crossentropy",
optimizer=keras.optimizers.SGD(learning_rate=1.5), metrics=[rounded_accuracy])
history = stacked_ae.fit(X_train, X_train, epochs=20,
validation_data=(X_valid, X_valid))
Reconstruction data
오토 인코더가 잘 훈련되었는지 비교하는 방법은 입력과 출력(재구성)을 비교하는 것이다.

fashion_mnist의 입력 데이터와 재구성 데이터를 비교했을 때,
재구성 데이터의 경우 식별은 할 수 있지만 정보를 많이 잃은 것을 확인할 수 있다.
입력 데이터와 재구성 데이터의 차이를 줄이기 위해서 모델을 더 오래 훈련하거나, 인코더/디코더의 레이어를 늘리거나, 코딩(latent space)의 크기를 늘리는 방법을 고려할 수 있다.
오토 인코더를 이용한 차원 축소
학습된 Deep autoencoder 모델은 차원 축소에 활용할 수 있다.
오토 인코더는 다른 차원 축소 알고리즘에 비해 좋은 결과를 만들어내지는 못하지만 대용량 데이터셋을 다를 수 있다는 장점이 있다.
따라서, 오토 인코더를 이용해 적절히 차원을 축소한 다음 다른 차원 축소 알고리즘을 고려해볼 수 있다.
np.random.seed(42)
from sklearn.manifold import TSNE
X_valid_compressed = stacked_encoder.predict(X_valid)
tsne = TSNE()
X_valid_2D = tsne.fit_transform(X_valid_compressed)
Unsupervised pre-training
레이블된 training data가 많지 않은 지도 학습 문제를 다룰 경우, 비슷한 문제를 학습한 신경망을 하위층에 재사용하는 것이 방법이 될 수 있다.(기존의 네트워크에서 학습한 특성 감지 기능을 재사용하는 것)
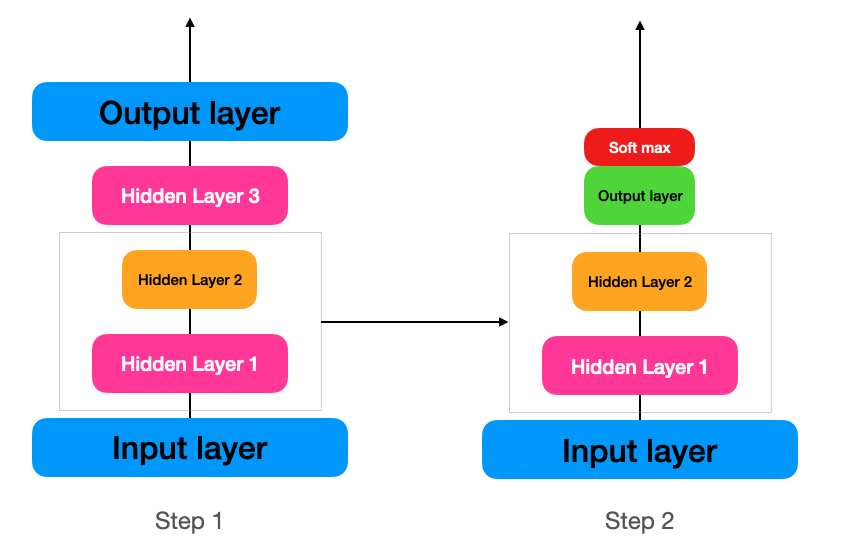
먼저 대부분 레이블되지 않은 학습 데이터를 전체를 deep autoencoder에 학습하고(step 1),
학습된 오토 인코더의 하위 layer(인코더 layer)를 실제 분류기의 layer로 구성(step 2)해 레이블된 데이터를 사용해 학습할 수 있다.
가중치 묶기
오토 인코더가 latent space를 기준으로 완벽하게 대칭일 경우, 디코더의 가중치와 인코더의 가중치를 묶는 것도 일반적인 방법이 될 수 있다.
가중치를 묶게 되면 가중치의 수가 절반으로 줄기 때문에 학습 속도도 높이고, overfitting될 가능성도 줄일 수 있기 때문이다.
오토 인코더가 입력층을 제외하고 N개의 층을 갖고, \(W_{L}\) 이 L번째 층의 가중치를 나타낸다고 했을 때,
디코더 층의 가중치는 \(W_{N-L+1} = W_{L}^{T}\) 로 정의할 수 있다.
class DenseTranspose(keras.layers.Layer):
def __init__(self, dense, activation=None, **kwargs):
self.dense = dense
self.activation = keras.activations.get(activation)
super().__init__(**kwargs)
def build(self, batch_input_shape):
self.biases = self.add_weight(name="bias",
shape=[self.dense.input_shape[-1]],
initializer="zeros")
super().build(batch_input_shape)
def call(self, inputs):
z = tf.matmul(inputs, self.dense.weights[0], transpose_b=True)
return self.activation(z + self.biases)
tied_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
dense_1,
dense_2
])
tied_decoder = keras.models.Sequential([
DenseTranspose(dense_2, activation="selu"),
DenseTranspose(dense_1, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
tied_ae = keras.models.Sequential([tied_encoder, tied_decoder])
Convolutional autoencoder
이미지를 다룰 때는 합성곱 신경망이 밀집 네트워크보다 훨씬 좋은 성능을 낼 수 있다.
인코더는 합성곱 층과 풀링 층으로 구성된 일반적인 CNN으로 입력 데이터에서 공간 방향의 차원(높이/너비)를 줄이고 깊이(특성 맵의 수)를 늘린다.
반대로 디코더는 이미지의 스케일을 늘리고 깊이를 원본 차원으로 되돌리는 역할을 수행한다.
conv_encoder = keras.models.Sequential([
keras.layers.Reshape([28, 28, 1], input_shape=[28, 28]),
keras.layers.Conv2D(16, kernel_size=3, padding="SAME", activation="selu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(32, kernel_size=3, padding="SAME", activation="selu"),
keras.layers.MaxPool2D(pool_size=2),
keras.layers.Conv2D(64, kernel_size=3, padding="SAME", activation="selu"),
keras.layers.MaxPool2D(pool_size=2)
])
conv_decoder = keras.models.Sequential([
keras.layers.Conv2DTranspose(32, kernel_size=3, strides=2, padding="VALID", activation="selu",
input_shape=[3, 3, 64]),
keras.layers.Conv2DTranspose(16, kernel_size=3, strides=2, padding="SAME", activation="selu"),
keras.layers.Conv2DTranspose(1, kernel_size=3, strides=2, padding="SAME", activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
conv_ae = keras.models.Sequential([conv_encoder, conv_decoder])
conv_ae.compile(loss="binary_crossentropy", optimizer=keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = conv_ae.fit(X_train, X_train, epochs=5,
validation_data=(X_valid, X_valid))Recurrent autoencoder
시계열이나 텍스트와 같은 시퀀스에 대해 순환 신경망을 이용해 오토 인코더를 만들 수 있다.
인코더는 입력 시퀀스를 하나의 벡터로 압축(Sequence - to - vector RNN)
디코더는 벡터를 시퀀스로 복원하는(Vector - to - sequence RNN)이다.
recurrent_encoder = keras.models.Sequential([
keras.layers.LSTM(100, return_sequences=True, input_shape=[28, 28]),
keras.layers.LSTM(30)
])
recurrent_decoder = keras.models.Sequential([
keras.layers.RepeatVector(28, input_shape=[30]),
keras.layers.LSTM(100, return_sequences=True),
keras.layers.TimeDistributed(keras.layers.Dense(28, activation="sigmoid"))
])
recurrent_ae = keras.models.Sequential([recurrent_encoder, recurrent_decoder])
recurrent_ae.compile(loss="binary_crossentropy", optimizer=keras.optimizers.SGD(0.1),
metrics=[rounded_accuracy])
Stacked denoising autoencoder
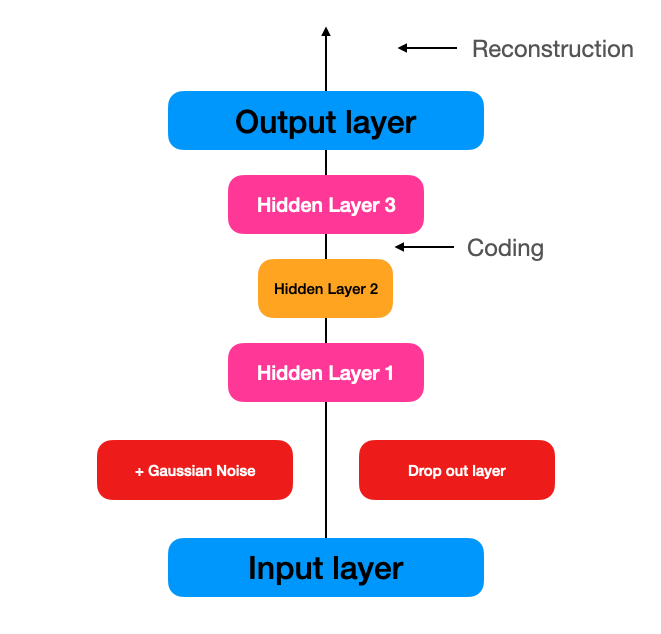
오토 인코더의 입력에 잡음 추가하고 잡음이 없는 원본 데이터로 복원하도록 훈련해 유용한 특성을 학습하도록 강제하는 방법
입력층과 hidden layer 사이에 가우시안 잡음을 추가하거나, 드롭아웃 층을 추가하여 구현할 수 있다.
tf.random.set_seed(42)
np.random.seed(42)
denoising_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.GaussianNoise(0.2),
keras.layers.Dense(100, activation="selu"),
keras.layers.Dense(30, activation="selu")
])
denoising_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation="selu", input_shape=[30]),
keras.layers.Dense(28 * 28, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
denoising_ae = keras.models.Sequential([denoising_encoder, denoising_decoder])
denoising_ae.compile(loss="binary_crossentropy", optimizer=keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = denoising_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))

Sparse autoencoder
오토인코더가 좋은 특성을 추출하도록 함다는 다른 제약의 방식은 회소성(Sparsity)를 이용하는 것이다.
비용 함수에 적잘한 항을 추가해 오토인코더가 코딩 층에서 활성화되는 뉴런 수를 감소시키게 만든다.
예를 들어 코딩 층에서 5%의 뉴런만 활성화되도록 강제한다면, 오토인코더는 5%의 뉴런을 조합해 입력을 재구성하기 때문에 유용한 특성을 표현할 수 있게 된다.
Sparse autoencoder를 구현하기 위해서는 학습 단계에서 코딩층의 실제 희소 정도를 측정해야 한다.
전체 학습 배치(batch)에 대해 코딩층의 평균적인 활성화 정도를 계산하고 손실함수에 희소 손실을 추가해 뉴런이 너무 활성화도지 않도록 규제할 수 있다.
희소 손실을 구하기 위해서는 MSE를 이용하는 방법이 있지만,
(예를 들어, 한 뉴런의 평균 활성화가 0.3이고 목표 희소 정도가 0.1이라면 비용 함수에 \((0.3 - 0.1)^{2}\) 를 추가)
쿨백-라이블러 발산(Kullback-Leibler divergence)를 이용하는 것이 실제 문제에서 더 적합할 수 있다.
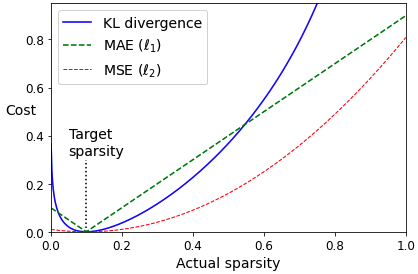
쿨백-라이블러 발산(Kullback-Leibler divergence)
https://daebaq27.tistory.com/88
[ML/DL] 쿨백-라이블러 발산 (Kullback-Leibler Divergence)
쿨백-라이블러 발산은 머신러닝이든 딥러닝이든 공부를 지속해가다보면 심심치 않게 만나볼 수 있는 개념이다. 공부를 할 때마다 위키피디아를 들락날락하지 않도록 블로그에 정리해보고자 한
daebaq27.tistory.com
KLD는 두 확률 분포 P와 Q의 차이를 계산하는데 사용되는 함수로
\(D_{KL}(P||Q)=\sum P(i)\log\frac{P(i)}{Q(i)} \)
KLD를 이용하면, 코딩 층에서 뉴런이 활성화될 목표 활률 p와 실제 확률 q 사이의 발산을 측정할 수 있다.
\(D_{KL}(p||q)=p\log \frac{p}{q} + (1-p)\log \frac{1-p}{1-q} \)
KLD를 이용해 각 뉴런에 대해 희소 손실을 계산하고, 이 손실들을 모두 합해 희소 가중치 하이퍼파라미터를 곱한다 다음,
비용 함수의 결과에 더해 최종 손실 함수 결과를 계산한다.
kl_divergence = keras.losses.kullback_leibler_divergence
class KLDivergenceRegularizer(keras.regularizers.Regularizer):
def __init__(self, weight, target=0.1):
self.weight = weight
self.target = target
def __call__(self, inputs):
mean_activities = K.mean(inputs, axis=0)
return self.weight * (
kl_divergence(self.target, mean_activities) +
kl_divergence(1. - self.target, 1. - mean_activities))
kld_reg = KLDivergenceRegularizer(weight=0.05, target=0.1)
sparse_kl_encoder = keras.models.Sequential([
keras.layers.Flatten(input_shape=[28, 28]),
keras.layers.Dense(100, activation="selu"),
keras.layers.Dense(300, activation="sigmoid", activity_regularizer=kld_reg)
])
sparse_kl_decoder = keras.models.Sequential([
keras.layers.Dense(100, activation="selu", input_shape=[300]),
keras.layers.Dense(28 * 28, activation="sigmoid"),
keras.layers.Reshape([28, 28])
])
sparse_kl_ae = keras.models.Sequential([sparse_kl_encoder, sparse_kl_decoder])
sparse_kl_ae.compile(loss="binary_crossentropy", optimizer=keras.optimizers.SGD(learning_rate=1.0),
metrics=[rounded_accuracy])
history = sparse_kl_ae.fit(X_train, X_train, epochs=10,
validation_data=(X_valid, X_valid))
Variational autoencoder
변이형 오토인코더는 다른 오토인코더와 비교해서 두가지 차이점이 있다.
- 확률적 오토인코더(Probabilistic autoencoder) : 학습이 끝난 후에도 출력이 부분적으로 우연에 의해 결정
- 생성적 오토인코더(Generative autoencoder) : 새로운 샘플 생성
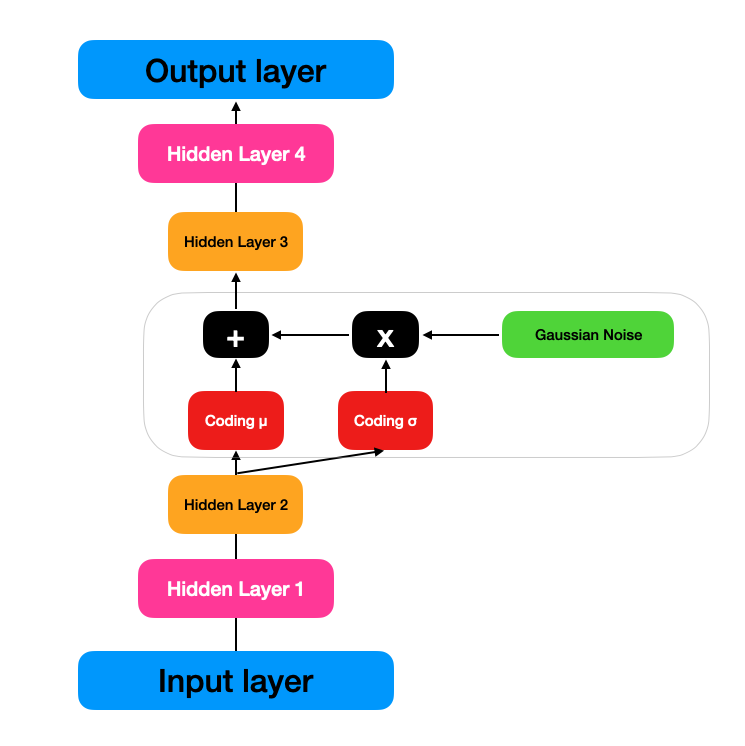
VAE는 기본적으로 다른 오토인코더와 같이 인코더와 디코더로 나누어져있다.
VAE가 다른 오토인코더와 다른 점은
주어진 입력에 대한 코딩을 바로 만드는 대신 인코더는 평균 코딩(mean coding) \(\mu\) 와 표준편차 \(\sigma\) 를 만들고,
실제 코딩은 평균이 \(\mu\)이고 표준편차가 \(\sigma\)인 가우시안 분포에서 랜덤하게 샘플링한다는 점이다.
이후 디코더는 샘플링된 코딩을 디코딩한다.
VAE는 입력이 매우 복잡한 분포를 가지더라도 간단한 가우시안 분포에서 샘플링된 것처럼 보이는 코딩을 만드는 경향이 있고,
학습하는 동안 손실 함수가 코딩을 가우시안 샘플들의 군집처럼 보이도록 latent space 안으로 점진적으로 이동시킨다.
따라서 VAE는 학습이 끝난 뒤 새로운 샘플을 매우 쉽게 생성할 수 있게 된다.
VAE의 손실 함수
VAE의 손실 함수는 오토인코더가 입력을 재생산하도록 만드는 일반적인 재구성 손실(reconstruction loss)과
단순한 가우시안 분포에서 샘플된 것 같은 코딩을 가지도록 오토인코더를 강제하는 잠재 손실(latent loss)로 구성된다.
잠재 손실은 목표 분포(가우시안 분포)와 실제 코딩 분포 사이의 KLD를 이용한다.
VAE의 잠재 손실의 경우 가우시안 잡음으로 인해 희소 인코더보다 수식이 복잡하다.
\( L = -\frac{1}{2}\sum_{i=1}^{n}1 + \log(\sigma_{i}^{2})-\sigma_{i}^{2}-\mu_{i}^{2}\)
( \(L\)은 잠재 손실, \(n\)은 코딩 차원, \(\mu_{i}\)와 \(\sigma_{i}\)는 \(i\)번째 코딩 원소의 평균과 표준 편차)
VAE의 인코더가 \(\sigma\)가 아닌 \(\gamma=\log(\sigma^{2})\) 출력하도록 변형하면 더 안정적이고 높은 성능의 VAE를 만들 수 있다.
L = -\frac{1}{2}\sum_{i=1}^{n}1 + \gamma_{i} - \exp(\gamma_{i}) - {\mu_{i}^{2}}
VAE 구현하기
VAE를 구현하기 위해서는 먼저 \(\mu\)와 \(\gamma\)가 주어졌을 때 코딩을 샘플링하는 함수를 구현해야한다.
class Sampling(keras.layers.Layer):
def call(self, inputs):
mean, log_var = inputs
return K.random_normal(tf.shape(log_var)) * K.exp(log_var / 2) + mean샘플링 함수는 \(\mu\)와 \(\gamma\)를 입력으로 받고, 평균이 \(\mu\)이고 표준편차가\(\sigma\)인 정규분포에서 코딩 벡터를 샘플링한다.
codings_size = 10
inputs = keras.layers.Input(shape=[28, 28])
z = keras.layers.Flatten()(inputs)
z = keras.layers.Dense(150, activation="selu")(z)
z = keras.layers.Dense(100, activation="selu")(z)
codings_mean = keras.layers.Dense(codings_size)(z)
codings_log_var = keras.layers.Dense(codings_size)(z)
codings = Sampling()([codings_mean, codings_log_var])
variational_encoder = keras.models.Model(
inputs=[inputs], outputs=[codings_mean, codings_log_var, codings])
decoder_inputs = keras.layers.Input(shape=[codings_size])
x = keras.layers.Dense(100, activation="selu")(decoder_inputs)
x = keras.layers.Dense(150, activation="selu")(x)
x = keras.layers.Dense(28 * 28, activation="sigmoid")(x)
outputs = keras.layers.Reshape([28, 28])(x)
variational_decoder = keras.models.Model(inputs=[decoder_inputs], outputs=[outputs])
_, _, codings = variational_encoder(inputs)
reconstructions = variational_decoder(codings)
variational_ae = keras.models.Model(inputs=[inputs], outputs=[reconstructions])인코더에서는 \(\mu\)와 \(\gamma\)를 출력하는 두 Dense layer가 동일합 입력(두번째 Layer의 출력)을 받아 출력값을 Sampling으로 전달한다.
latent_loss = -0.5 * K.sum(
1 + codings_log_var - K.exp(codings_log_var) - K.square(codings_mean),
axis=-1)
variational_ae.add_loss(K.mean(latent_loss) / 784.)
variational_ae.compile(loss="binary_crossentropy", optimizer="rmsprop", metrics=[rounded_accuracy])
history = variational_ae.fit(X_train, X_train, epochs=25, batch_size=128,
validation_data=(X_valid, X_valid))잠재 손실과 재구성 손실을 추가해서 VAE를 구현할 수 있다.
VAE로 새로운 데이터 생성
codings = tf.random.normal(shape=[12, codings_size])
images = variational_decoder(codings).numpy()
참고
https://excelsior-cjh.tistory.com/187
08. 오토인코더 (AutoEncoder)
이번 포스팅은 핸즈온 머신러닝 교재를 가지고 공부한 것을 정리한 포스팅입니다. 08. 오토인코더 - Autoencoder 저번 포스팅 07. 순환 신경망, RNN에서는 자연어, 음성신호, 주식과 같은 연속적인 데
excelsior-cjh.tistory.com
출처
https://www.hanbit.co.kr/store/books/look.php?p_code=B9267655530
핸즈온 머신러닝
최근의 눈부신 혁신들로 딥러닝은 머신러닝 분야 전체를 뒤흔들고 있습니다. 이제 이 기술을 거의 모르는 프로그래머도 데이터로부터 학습하는 프로그램을 어렵지 않게 작성할 수 있습니다. 이
www.hanbit.co.kr