[논문 리뷰] DR3 : Value-Based Deep Reinforcement Learning Requires Explicit Regularization (ICLR 2022)
DR3 : Value-Based Deep Reinforcement Learning Requires Explicit Regularization (ICLR 2022)
논문 : https://openreview.net/forum?id=POvMvLi91f
DR3: Value-Based Deep Reinforcement Learning Requires Explicit...
Despite overparameterization, deep networks trained via supervised learning are surprisingly easy to optimize and exhibit excellent generalization. One hypothesis to explain this is that...
openreview.net
발표 영상 : https://www.youtube.com/watch?v=P7bygduR4hc
Abstract
1) Supervised Learning의 성과
- Deep neural network의 over-parameterization에도 불구하고, supervised learning을 통해 학습된 Deep Neural network는 최적화하기 쉽고 뛰어난 일반화 성능을 보여주고 있음
- over-parameterization : Deep Learning Model이 학습할 때 사용되는 parameters(weight 및 bias)의 수가 모델의 복잡도에 비해 상대적으로 많을 때 발생하는 현상
- Over-parameterized 심층 신경망이 Stochastic Gradient Descent로 유도된 implicit regularization로 일반화된 Solution을 제공
- Implicit Regularization : 모델의 학습 과정에서 자연스럽게 발생하는 정규화 기법 (e.g. Stochastic Gradient Descent, Drop Out, Early Stopping 등)
- Explicit Regularization : 모델의 복잡성을 줄이고 과적합을 방지하기 위해 명시적으로 추가되는 정규화 항목 (e.g. L1 정규화, L2 정규화)

How millions of parameters can avoid overfitting
Both linear regression and deep learning can leverage a massive number of mis-specified features
medium.com
2) Implicit Regularization을 Offline Reinforcement Learning에 적용하면, Supervised Learning처럼 좋은 성과를 보일 수 있을까?
- Supervised Learning에서 관찰되는 Stochastic Gradient Descent의 implicit regularization 효과가 Offline RL 환경에서 오히려 Offline Reinforcement Learning의 일반화 성능이 떨어지고, 비정상적인 Feature representation을 야기시킴
- 기존의 implicit regularization이 TD Learning(Temporal-Difference Learning)에 적용될 때, Regularizer가 과도하게 aliasing된 degenerate soultion을 제공 (Supervised Learning과 대조)
- aliasing : Neural Network Model에서 특정 입력값 또는 상태와 관련된 정보를 잘못 해석하는 것
- Bootstrapping을 통해 학습된 심층 신경망 기반 value function이 degenerate됨. (Bellman backup 에서 state-action이 aliasing)에 의해 학습된 특징 표현이 비정상적으로 됨.
- Bootstrapping in RL : Reinforcement Learning에서 Bootstrapping이란, 예측값을 이용해 또 다른 값을 예측하는 것
- $Q(s,a) \leftarrow Q(s, a) + \alpha (R_{t+1} + \gamma Q(s',a') - Q(s,a))$
- 위의 수식에서 $R_{t+1} + \gamma Q(s',a')$는 Optimal $Q(s, a)$의 예측값이고, 이 예측값을 $Q(s,a)$를 예측하는데 사용. 따라서 DQN에서 Q value update는 boostrapping method
3) 제안 : DR3 Regularizer
- 2)에서 제시한 문제점들을 해결하기 위해 implicit regularizer의 형태를 도출하고, implicit regularizer의 원치 않는 영향을 상쇄시킨 Explicit Regularzier 제안 (DR3)
1. Introduction
1) 질문 : Supervised Learning에서 관찰되는 implicit regularization 효과가 Reinforcement learning에도 적용될까?
- 심층 신경망은 수십억 개의 Parameter를 가지고 있는데 원칙적으로 overfitting에 취약한 구조
- 그럼에도 불구하고 Deep neural network를 사용한 supervised learning이 잘 일반화되는 이유는 다양한 implicit regularization 효과에 기인
- 그렇다면 Deep neural network를 reinforcement learning에서 사용하면 동일한 이유로 잘 작동할까?
2) 목표 : implicit regularization이 Deep value function의 성능 저하를 유도하는 원인을 분석하고 이에 대한 해결책을 제시
- implicit regularization은 over-parameterized-deep neural nets value function을 학습할 때, poor learned representations를 유발
- exploration과 non-stationary data distribution으로 인해 confounding effects를 배제하기 위해 offline RL으로 제한
- Offline Reinforcement learning의 Deep value function은 반드시 오프라인 데이터(static dataset of experience)에서 학습되어야 함
- Confounding effect : y의 원인이 x라고 하고 싶은데, x와 y에 동시에 영향을 주는 제 3의 변수 z가 존재할 때 Confounding effect가 발생하고, 변수 z를 confounding factor 또는 confounder라곡 부름
- 선행 연구에서 Offline deep neural nets. RL으로 학습된 value function은 성능이 저하된다는 것과 low-rank features의 출현에 관련되어있다는 것을 밝힘
- 본 연구의 목표는 bootstrapping 중에 poor representations이 나타내는 근본적인 원인을 이해하고 잠재적인 해결책을 개발하는 것
- 이 원인을 해결하기 위해, TD learning으로 Deep value function을 학습할 때 발생하는 implicit regularizer를 Characterize함
- implicit regularizer의 형태는 TD learning이 state-action에서 feature representations을 co-adapt한다는 것을 의미
3) 제안 : State-Action 에서 feature representations가 co-adaptation 되는 현상을 방지할 수 있는 DR3 Regularizer 기법
- aliasing 현상이 실제로는 feature "co-adaptation"으로 나타남.
- Q-value network에 의해 학습된 연속적인 state-action의 features가 dot-product 측면에서 매우 유사
- co-adaptation으로 학습된 모델은 일반적으로 낮은 성능으로 수렴
- Q-value가 over-estimation되지 않더라도 Offline RL에서 prolonged learning은 feature co-adaptation의 증가로 인한 성능 저하로 이어짐
- implicit regularization의 결과로 발생하는 co-adaptation 문제를 완화하기 위해, DR3라고 불리는 explicit regularizer를 제안
- 이론적으로 유도된 implicit regularizer의 효과를 정확하게 추정하는 것은 계산적으로 어려움
- DR3는 state-action의 features를 dot-product similarity 측면에서 정규화를 통해 co-adaptation 문제를 완화하는 approximation 제공
- 실험적으로 DR3는 feature rank collapse와 같은 이전에 언급된 pathologies을 방지
- 또한 실제로 사용되는 기본 offline reinforcement learning에 비해 더 오래 학습할 수 있는 방법을 제공하고 성능을 향상시킴

4) 기여점
(1) 기여 1
- TD learning으로 deep value function을 학습할 때 발생하는 implicit regularization과 Offline deep RL에서 co-adaptation 문제를 일으킨다는 것을 이론적으로 증명
- Feature adaptation은 장기간 학습으로 인한 성능 저하를 포함한 offline deep RL의 challenge 중 하나
(2) 기여 2
- Offline reinforcement learning을 위한 간단하고 효과적인 explicit regularizer 기법인 DR3 제안
- 이는 bootstrapping update에서 나타나는 state-action의 feature 유사성을 최소화
- DR3는 REM, CQL, BRAC과 같은 기존 오프라인 강화학습 알고리즘과 쉽게 결합
2. Preliminaries
1) Standard RL
- 강화학습의 목표 : Markov Decision Process에서 long-term discounted reward를 최대화
- $(S, A, R, P, \gamma)$로 표기
- $S$ : state space
- $A$ : action space
- $R$ : reward function $R(s, a)$
- $P$ : 상태 전이 확률 $P(s'|s, a)$
- $\gamma$ : 감가율 $\gamma \in [0, 1)$
- policy $\pi(a|s)$를 위한 Q-function $Q^\pi(s,a)$ : 정책 $\pi(a|s)$을 따라서 상태 s에서 행동 a를 수행했을 때 얻을 수 있는 expected sum of discounted rewards.
- $Q(s,a) := R(s, a) + \gamma E_{s' \sim P(\cdot |s,a),a' \sim \pi(\cdot |s')}[Q(s',a')]$
- Q 함수는 파라티머 $\theta$로 구성된 신경망을 Parameteraization
- Standard deep RL은 Bellman equations을 $Q_\theta$를 위한 squared temporal difference(TD) error objective로 변환
- $L_{TD}(\theta) = \sum_{s,a,s' \sim D}((R(s, a) + \gamma \bar{Q}_\theta (s',a')) - Q_\theta(s,a))^2$
- 이때 $\bar{Q}_\theta$는 target Q-network를 의미. 그리고 행동 $a'$는 상태 $s'$에서 target Q-network를 최대화함으로써 계산되는 값
- 이때 Deep neural network의 penultimate layer의 학습된 features를 다음과 같이 표기 : $\pi_\theta (s,a)$
- 이에 따라 Q function의 출력 값을 다음과 같이 표기 가능 : $Q_\theta (s, a) = w^T \pi (s, a)$ 이때, $w$는 마지막 출력층 layer의 가중치 파라미터
- penultimate layer : neural network 구조에서 뒤에서 두 번째에 위치한 layer로, 고차원의 데이터 표현을 포함한 출력으로 다양한 작업을 수행 가능
2) Offline RL
- Offline reinforcement learning algorithm은 반드시 주어진 데이터셋 $D=(s_i,a_i,s'_i,r_i)$만을 사용해 policy를 학습해야 함. 이 데이터셋은 active data cllection 없이, 어떠한 behavior policy $\pi_\beta(a|s)$에 의해 생성
- Offline reinforcement learning에서 주요 문제점은 learned policy와 behavior policy 간의 distributional shift 문제
- 본 연구의 목표는 시간차 학습에서 implicit regularization의 효과를 연구하는 것이지 distributional shift 문제를 해결하는 것이 아님
- 따라서 본 연구의 실험은 기존의 오프라인 강호학습 방법론을 기반으로 작업
- CQL(Conservative Q-Learning) : 학습 도중에 잘못된 Q-value에 패널티를 줌
- REM(Random Ensemble Mixture) : Q-function의 ensembel을 활용
- BRAC(Behavior Regularized Actor Critic) : policy constratins를 적용
3. Implicit Regularization in Deep RL via TD-Learning
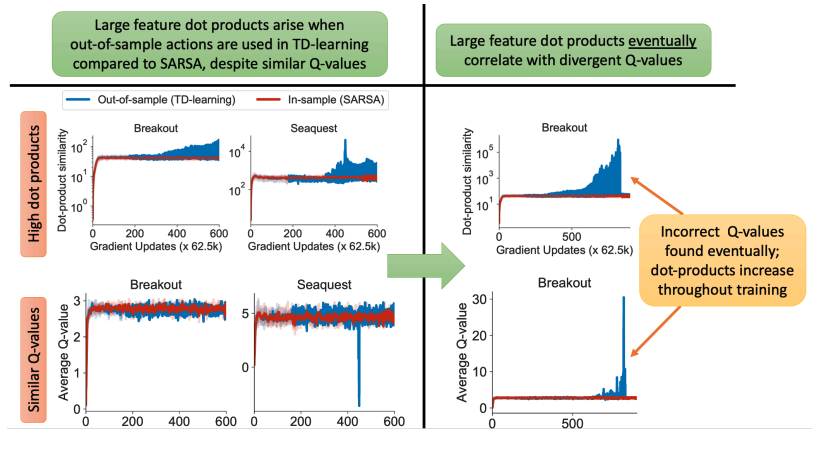
- 유사한 Q 값에도 불구하고 SARSA와 비교하여 TD learning에서 out-of-sample에서 high dot products 발생
- 그림에서 feature 내적 $\phi (s, a)^{T} \phi (s', a') $은 sample 외부에서는 학습 중 증가하는 경향을 보이고, Average Q-value는 수렴하면서 상대적으로 일정하게 유지
- 관측된 state-action으로 backups (offline SARSA) 하거나, Bellman backups (i.e., supervised regression)을 하지 않을 경우에는 안정적이고 상대적으로 낮은 내적으로 이러한 문제점을 피할 수 있음
- (Left: 높은 feature 내적은 사용한 TD learning은 결국 불안정해지고 잘못된 Q-value를 만들어냄.)
- (Right: Q-value가 안정적인 추세에도 불구하고 DQN은 매우 큰 feature 내적을 얻음)
- Deep Q-network의 TD error를 최소화함으로써, 본 연구는 implicit regularization이 Bellman backup에 나타나는 state-action representation을 co-adaptate한다는 것을 시사한다.
3.1 Feature Co-Adaptation and How It Relates to Implicit Regularization
- "Feature co-adaptation" 현상을 실험적으로 제시
- 이 현상은 bootstrapping을 통해 value function을 학습할 때 발생하고 이 현상으로 인해 연속적인 state-action tuple의 feature representations에서 dot product $\pi(s,a)^T \pi (s',a')$의 값이 커지게 됨
1) Experimental Setup
- 공통
- 2개의 Atari 게임(Breakout, Seqauest)에서 DQN의 replay buffer에서 균일하게 샘플링된 데이터의 1%로 이루어진 오프라인 데이터셋 이용
- 아래의 비교 모델을 통해 feature dot products $\pi(s,a)^T \pi(s',a')$ 값을 확인
- 또한 데이터셋 전체에 대한 Q-Network의 Average Q-value를 추적하여, 해당 값이 발산하는지 혹은 안정적인지 측정
- 비교 모델 1: Supervised Regression
- 몬테 카를로 반환 추정치에 대한 supervised regression을 통해 Q-function 학습
- 비교 모델 2: Offline SARSA
- behavior policy의 value $Q^{\pi_\beta}$를 추정하는 것이 목표
- 데이터셋 구성 : $(s, a, r, s', a') \in D$. TD learning과 달리, 다음 상태 $s'$에서 실제로 수행한 action $a'$가 데이터셋에 포함
- 비교 모델 3: Offline TD-Learning
- behavior policy의 value $Q^{\pi_\beta}$를 추정하는 것이 목표
- 다음 state $s'$에서 action $a'$는 behavior policy $\pi_\beta$에 의해 샘플링: $a' \sim \pi_\beta (\cdot | s')$
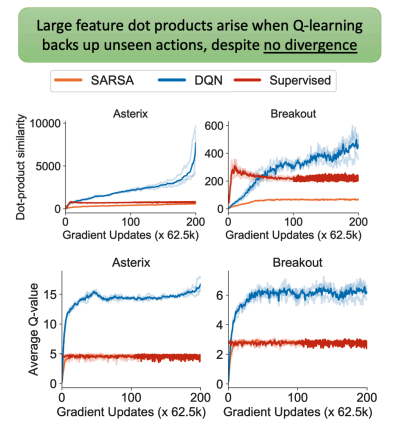
2) Observing Feature co-adaptation empirically
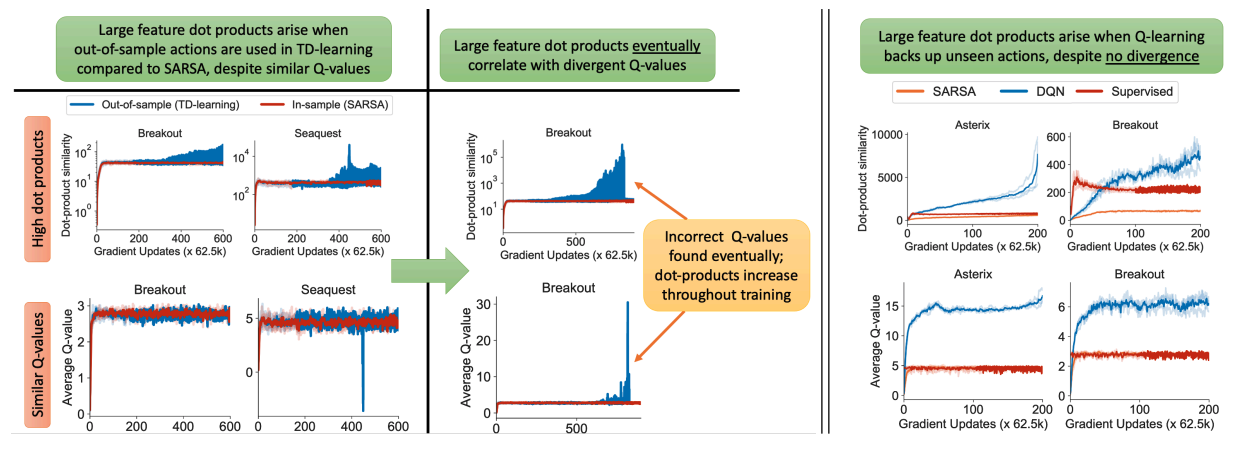
- 그림 2.에 표시된 것처럼 state-action의 feature 간 내적(맨 위 행)은 Q-learning과 TD-learning 모두에 대해 지속적으로 증가
- 반면 supervised regression에서는 작은 값으로 수렴
- 이것이 단순히 Q-learning이 수렴하지 못한 경우라고 생각할 수도 있지만, 아래 행에서 Q-learning의 평균 Q-value가 실제로 수렴
- 그럼에도 불구하고 최적화 모델은 더 높은 feature의 내적을 향해 네트워크를 학습
- state-action 의 feature 간 내적을 최대화하려는 암시적 현상을 "feature co-adaptation"이라고 부름
4) When dose feature co-adaptation emerge?
- 그림 2.에서 오프라인 SARSA의 feature 내적은 supervised regression과 유사하게 빠르게 수렴하고 안정적
- 이는 bootstrapping update만으로는 내적의 증가와 불안정성과는 관련이 없음을 나타내는데, 오프라인 SARSA가 Bellman Backups 사용하지만 결과는 supervised regrssion의 결과와 유사하기 때문
- TD-learning도 SARSA와 마찬가지로 behavior policy를 추정하기 때문에 SARSA 일치해야하지만 TD-learning에서는 feature co-adaptation이 발생
- 차이점은 $a'$의 출처
- Offline SARSA는 항상 학습 데이터 집합에서 관찰된 행동 $a'$를 학습에 사용
- 반면 Offline TD-Learning은 학습 데이터 집합에서 본적 없는 행동 $a'$를 학습에 사용하며, 이는 데이터 생성 정책의 분포 내에 존재
- 이것이 Bellman Backup에서 "out-of-sample"행동을 활용하는 것이 out-of-distribution이 아닐지라도, learning dynamics을 크게 변경하기 때문
* Bellman Optimality Equation
- backup : next state-value function으로 현재의 value function을 구하는것
- step에 따라 "one step backup", "multi step backup"
- state에 따라 "full width backup(가능한 모든 다음 state의 value fuction을 사용하여 backup)", "sample backup(실제의 경험을 통해서 backup)"
- cf) dynamic programming : value function을 구할 때 바로 다음 step의 value function을 이용하기에 one step backup이고 현재 s에서 가능한 모든 s'의 value function을 구하기 때문에 full width backup
- Bellman Optimality Equation : optimal policy를 따르는 bellman equation으로 최대의 reward를 갖는 value fuction
3.2 Theoretically Characterizing Implicit Regularization in TD Learning
- TD learning에서 feature co-adaptation이 나타나는 이유와 out-of-sample action과 어떤 관련이 있는지 알기위해서는 TD-learning의 implicit regularization을 characterize해야함
Background
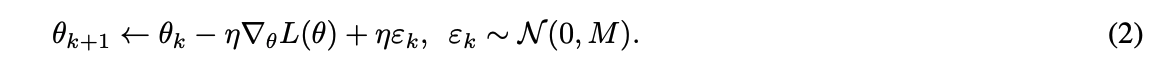
- Squared loss을 사용하는 supervised learning $ f_{\theta }(x) $를 학습할 때, over-parameterization으로 인해 training set에서 다양한 $\theta $에 대해 $L(\theta )= 0$를 충족
- SGD는 특정 방향(Hessian space)을 따라 $ \triangledown \theta R(\theta^{*}) = 0 $을 만족하는 fixed point $\theta $를 찾음
- $R(\theta )$가 implicit regularizer이며, 여기서 도출된 noisy gradient updates form은 식 (2)와 같음
In Study
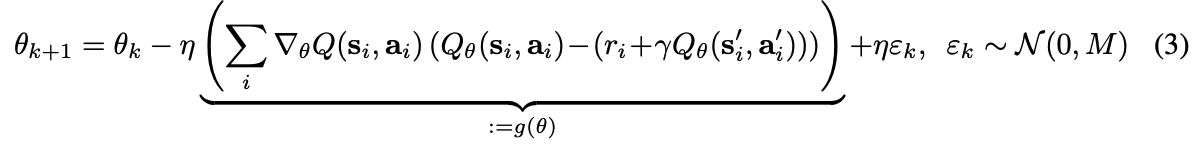
- SGD에서 찾은 프레임워크를 이용해 noisy TD learning의 fixed point를 분석
- noise covariance M으로 noisy pseudo-gradient TD update
- $\theta^{*}$는 training TD error의 안정적인 fixed point를 나타내며, $g(\theta_{*})=0$은 pseudo-gradient
- $\theta$에 대한 $g(\theta )$의 도함수를 행렬 $G(\theta ) \in R|\theta | \times |\theta |$로 표시하고 pseudo-Hessian이라 부름
- $G(\theta )$는 실제 잘 동작하는 2차 도함수는 아니지만 Gradient descent에서 Hassian matrix와 비슷한 역할
Assumptions
- 분석을 단순화하기 위해 행렬 G와 M이 d차원 공간에서 n차원 기반에 걸쳐있다고 가정(?).
- d는 매개변수의 수이고, n은 데이터 수. over-paramterized로 인해 n < d
- $\theta^{*}$에 대해 유도된 implicit regularizer를 도출하기 위해 $\theta^{*}$에서 초기화된 noisy TD learning(수식 3.)의 learning dynamics를 분석
- 다양한 update에서 noisy update가 $\theta^{*}$에 가깝에 유지되는 조건을 도출
- Theorem 3.1의 두 조건을 발생시킴
Theorem : Implicit regularizer at TD fixed points

- implicit regularizer for noisy GD in supervised learning : 지도 학습에서의 implicit regularizer에 해당
- additional term in TD learning : co-adaptation과 poor-representation을 유도하는 원인
- Condition (1)이 충족되지 않으면 매개변수가 적은 TD도 $\theta^{*}$에서 멀어지고, parameter space의 모든 방향에 대해 만족되면 over-parameterization으로 인해 고유값 $\lambda i (G)$의 실수부와 허수부가 모두 0인 방향이 존재
이러한 방향에서 학습은 tensor $\triangledown G$의 noise projection에 의해 제어되며, $\theta^{*}$ 주변의 $\theta_{k} - \theta^{*}$의 테일러 전개에 의해 나타남
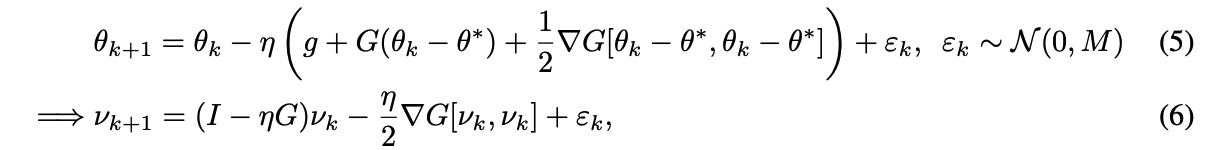
- 여기서 $v_{k} := \theta_{k} - \theta^{*}$의 관점에서 다시 매개변수화
- 증명은 $\theta^{*}$가 implicit regularizer $R_{TD}$(Condition (2))의 정지점인 경우 안정적이라는 것을 보여줌
- 이는 $\triangledown G$에 의해 누적된 총 noise(즉, $k$에 걸쳐 누적된 $\epsilon_{k}$)가 큰 문제로 이어지지 않도록 보장
Explaining the difference between utilizing seen and unseen actions in the backup.
- 오프라인 SARSA는 Bellman update 모든 state-action $(s'_{i}, i'_{i})$이 내적을 늘리는 방향으로 학습이 진행되지만, gradient norm을 줄이기위해 affinity로 균형을 이룸
- 예를 들어, $(s'_{i}, a'_{i})$가 $(s_{i}, a_{i})$의 순열일 경우 $R_{TD}$는 $(1- \gamma) \sum_{i} || \triangledown_{\theta} Q_{\theta} ( x_{i} ) ||_{2}^{2}$ 하한선이 지정되므로, $R_{TD} (\theta)$를 최소화하는 것은 내적을 최대화하는 대신 feature norm을 최소화함
- 이는 지도 학습을 통해 Q-function를 학습할 때 얻을 수 있는 implicit regularization에 해당하므로 분석에서는 in-sample $((s', a') \in D )$이 있는 오프라인 SARSA가 supervised regression과 유사하게 동작
- 그러나 관측되지 않은 state-action $(s'_{i}, a'_{i})$ 나타나는 경우 regularizer는 매우 다르게 작동
- $ a'$가 data set이 아닌 Deep RL 알고리즘에 의해 발생된 값
- 이 경우, $R_{TD} (\theta)$를 최소화하기 때문에 $(s, a)$와 $(s', a')$ 내적은 fixed-point 큰 값을 가짐(co-adaptation의 한 형태)
- out-of-sample의 state-action 기울기의 내적으로 관측된 state-action상태-동작 기울기와 매우 유사
Why is implicit regularization detrimental to policy performance?
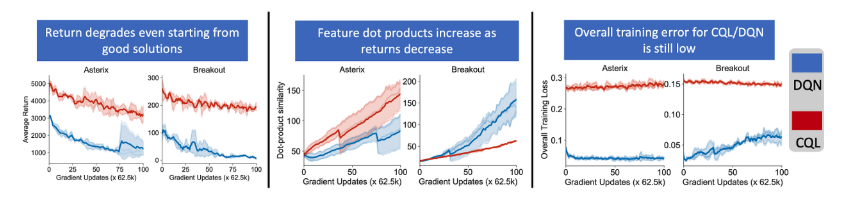
- 왜 implicit regularizeration이 정책 성능에 해로울까?
- implicit regularization이 부정적인 영향을 끼친다는 "경험적" 증거
- pre-trained DQN과 CQL을 실험 모델로 사용할 때, pre-trained 모델은 feature dot-product 값이 상대적으로 작음(그림 8.의 두번째 그래프)
- 이 실험의 목표는 이러한 "좋은" 초기 상태에서 시작하는 TD updates가 여전히 그 주변에 머무르거나, 더 나쁜 해결책으로 발산하는지 확인하는 것
- 그림 8.의 첫번째, 두번째 그래프에서 확인할 수 있듯이, policy의 성능(Average Return)이 즉시 악화되며, Dot-product similarity가 증가하기 시작하고 심지어 Learned Policy와 Behavior Policy 사이의 distributional shift를 명시적으로 보정하는 CQL에서도 이러한 현상이 발생
- 이는 전형적인 out-of-distribution action 설명으로 직접적으로 설명할 수 없다는 것을 시사
- 이러한 성능 하락의 원인은 그림 8.의 세번째 그래프에서 보듯이 CQL과 DQN 모두 Loss function의 값이 일반적으로 작은 것을 볼 수 있고, 이는 feature dot product를 증가시키려는 경향이 TD error를 최소화하지 못함으로 설명되지 않는다는 것을 나타냄.
- DR3 regularizer를 사용했을 때, 이러한 성능 저하를 효과적으로 완화할 수 있음.

- implicit regularization이 부정적인 영향을 끼친다는 "이론적" 증거
- Proposition 3.2는 co-adaptation의 결과로 인해 TD-Learning이 수렴하지 않을 수도 있다는 것을 의미
4. DR3 : Explicit Regularization for Deep TD-Learning
1) 개요
- TD Learning에서 implicit regularization 효과가 feature co-adaptation으로 이어질 수 있으며, 이는 결과적으로 성능 저하와 관련될 수 있음. 이 문제를 해결하기 위한 explicit regularization을 도출해야함
- 본 연구에서는 수식 2.의 두번째 항을 상쇄하는 explicit regularization을 제안. 두번째 항이 그대로 남아있으면 co-adaptation과 poor representations으로 이어질 것
- 2개의 implicit regularizer의 차이를 상쇄하는 explicit regularizer는 수식 4.와 같음. 이는 $R_{TD}(\theta)$의 두번째 term을 나타냄.
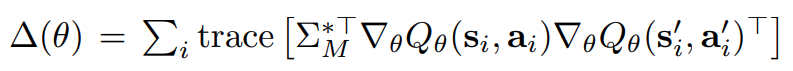
- DR3는 다양한 오프라인 강화학습 알고리즘과 결합될 수 있음.
- 이에 대한 학습 Object는 다음과 같이 정의
- $L(\theta ) := L_{A_{LG}}(\theta ) + c_{0} \triangle (\theta )$
- $L_{A_{LG}}(\theta )$ : 오프라인 강화학습 알고리즘의 Object
- $c_{0}$ : DR3 Term의 계수
2) Practcal version of DR3
- DR3를 실제로 구현하기 위해서는 특정한 Noise model을 선택해야 함
- 일반적으로 모델의 "올바른" 선택을 미리 알기는 어렵고, 이는 데이터 분포의 복잡한 함수, neural network 아키텍쳐 그리고 initialization 문제
- 따라서 DR3를 2개의 heuristic choices으로 구체화
- 지도 학습에서 연구된 label noise로 인한 모델 선택. 이 모델에 대한 계산적으로 무거운 fixed-point 연산이 필요
- $\sum_{M}^{*} = I $ 로 설정하는 더 간단한 대안 선택
- 위 2가지 변형이 기존 오프라인 강화학습보다 일반적으로 성능을 향상시킨다는 것을 발견
- 두번째 방법의 계산 비용이 더 낮기 때문에 노이즈 모델로 실제로 사용
- 또한, 각 변형의 gradient dot-product를 계산하고 back-propergation하는 것은 연산 속도가 느림. 따라서 $\delta (\theta )$를 계산할 때 마지막 레이어 매개변수에서의 contribution만 고려하는 근사치로 대신
- Practical version of DR3는 label noise 버전과 유사하게 작동하며, 수식 5.와 같음
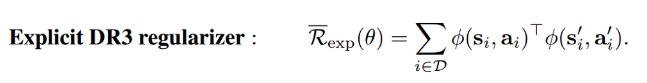
5. Experimental Evaluation of DR3
1) 개요
- 실험 목표
- DR3가 Offline RL에서 실제로 어떻게 성능을 향상시키는지 평가
- 기존의 rank collapse의 미치는 영향 연구
- 실험 환경
- Atari 2600 게임 : discrete actions
- D4RL : continuous actions
- image-based robotic manipulation tasks
2) Offline RL on Atari 2600 games
- 3 종류의 데이터셋에서 평가
- DQN replay buffer의 데이터 중 1%만 랜덤하게 샘플링 데이터셋
- DQN replay buffer의 데이터 중 5%만 랜덤하게 샘플링 데이터셋
- online DQN에서 관찰된 처음 10%만 샘플링된 sub-optimal 데이터셋
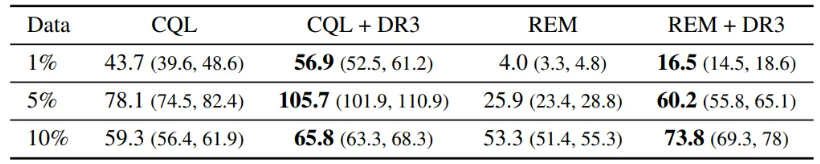
- 테이블 1.은 IQM(Interquartile mean) average performance
- 테이블 1. 에서 모든 데이터셋에 대해 DR3가 적용된 CQL, REM에서 성능 향상을 볼 수 있음
- CQL+DR3는 CQL 대비 최종 20%, 평균 25% 성능 향상
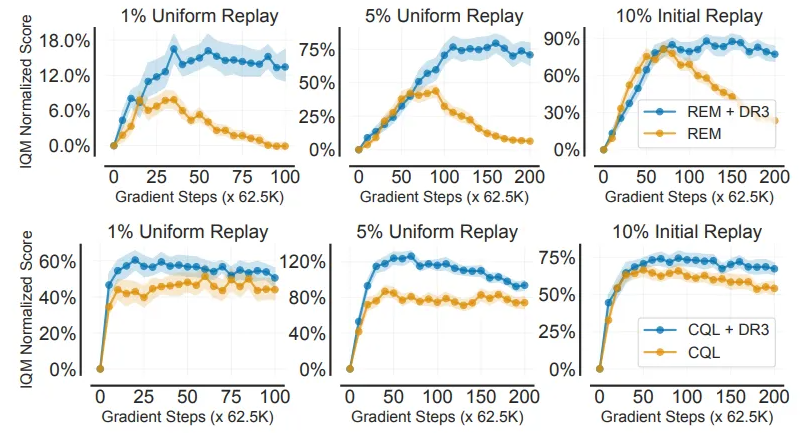
- 그림 9는 학습 동안의 17개의 게임에 대한 IQM normalized score
- REM은 학습이 진행될수록 성능 저하를 보이지만, DR3가 이를 방지(그림 9. top)
- DR3는 기존의 Offline RL Algorithm(CQL, REM)에 비해 상대적으로 안정적임을 확인
3) Offline RL on robotic manipulation from images

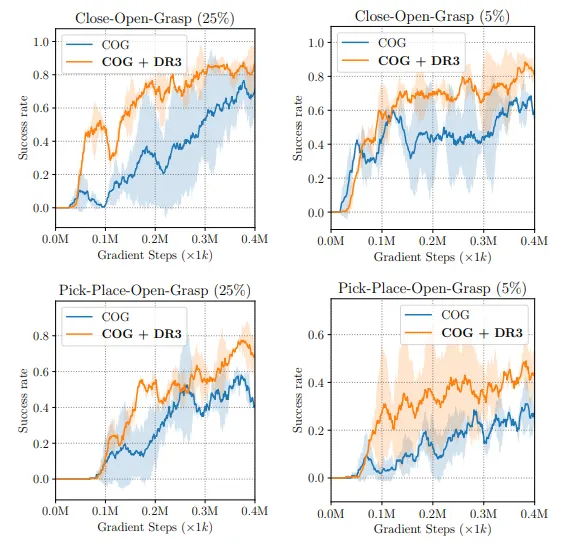
tt
- task의 reward는 오직 sparse하게 0 또는 1을 제공
- 그림 11.에서 보는것처럼, COG+DR3의 성능이 COG보다 높음
4) Offline RL on D4RL tasks

- DR3가 안정적이며 CQL에서 나타나는 최종적인 학습 손실을 방지할 수 있는지 평가하기 위해 해당 실험은 2M, 3M에 대한 학습 진행
- 테이블 2.에서 보는 것처럼 CQL+DR3가 우수함을 확인
5) DR3 does not suffer from rank collapse
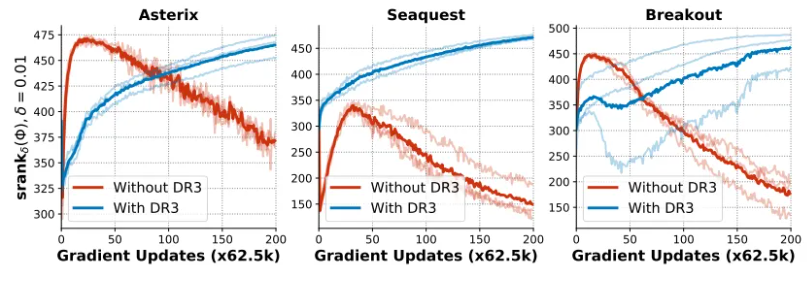
- DR3를 적용했을 때, rank collapse에 빠지지않는 것을 확인할 수 있음
6) Comparing explicit regularizers for different chices of noise covariance M
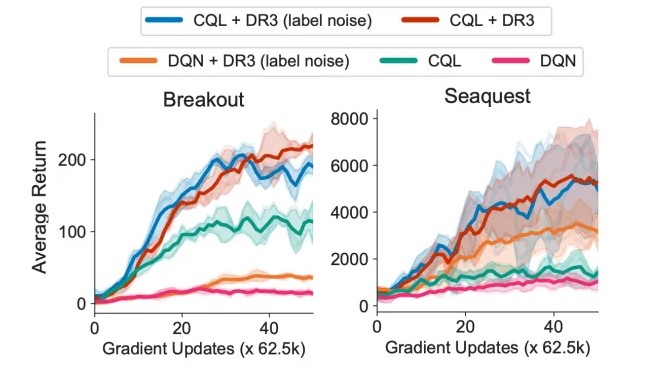
- CQL+DR3(label noise)와 CQL+DR3의 성능이가자장 우수
- noise model을 $\sum^{*}_{M}=I$로 설정하면 label noise에 비해 연산량은 줄면서 성능은 비슷
7) Discussion
- TD learning의 implicit regularization은 Bellman backup에서 나타나는 연속적인 state-action tuple의 feature를 co-adapt하려는 경향을 가지고 있음
- 이러한 regularization 효과는 Bellman backup에 out-of-sample을 사용할 때 악화되며, policy 성능의 저하로 이어짐
- 이에 본 연구에서 Practical explicit regularizer인 DR3를 제안하므로써, 다양한 offline RL problem에서 학습의 안정성과 성능 향상을 증명