특정 자료구조를 사용했을 때의 시간 복잡도나 내부적으로 어떻게 동작하는 지 구체적으로 알고 있는 것도
중요하다는 것을 이번에 뼈저리게 느꼈다
이진 탐색 트리는 이진 트리로 만들어진 탐색을 위한 자료구조이다. 4가지 조건을 가진다.
1. 이진 탐색 트리의 4가지 조건
1) 모든 노드의 키는 유일하다.
2) 왼쪽 서브트리의 모든 키는 루트 노드의 키보다 작다
3) 오른쪽 서브트리의 모든 키는 루트 노드의 키보다 크다
4) 서브트리도 이진탐색트리이다.
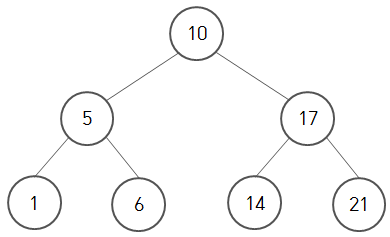
2. 이진 탐색트리의 동작 방식
1) 탐색(Search)
위의 이진 탐색 트리에서 14라는 키 값을 찾는다고 생각하면
루트노드 10과 비교했을 때, 14가 더 큼으로 오른쪽 서브 트리로 이동
오른쪽 서브 트리의 루트노드 17과 비교했을 때, 14가 더 작음으로 왼쪽 서브 트리로 이동
2) 삽입(Inseart)
삽입은 BST의 조건을 깨지 않기 위해서, 단말노드에 값을 추가해주는 방식이다.
위의 이진 탐색 트리에서 12를 추가한다고 하면,
루트노드 10과 비교했을 때, 12가 더 큼으로 오른쪽 서브 트리로 이동
오른쪽 서브 트리의 루트노드 17과 비교했을 때, 12가 더 작음으로 왼쪽 서브 트리로 이동
왼쪽 서브 트리의 루트노드 14와 비교했을 때, 12가 더 작음으로 왼쪽 서브트리의 루트 노드로 연결
3) 삭제(Delete)
삭제는 3가지 케이스로 나눌 수 있다
a. 삭제할 노드의 자식 노드가 없을 때,
단순히 부모 노드와의 링크만 끊어 주면 된다
자바는 GC가 알아서 메모리 회수해주므로 링크만 끊으면 되지만
C/C++은 free() 사용해서 메모리 회수해줘야한다
b. 삭제할 노드의 자식 노드가 하나 있을 때,
삭제되는 노드의 자식 노드와 부모 노드를 연결하도록 링크만 조절하면 된다
c. 삭제할 노드의 자식 노드가 두 개 있을 때,
삭제할 노드의 값을 삭제하고 매꿔줘야하는데,
중위 순회했을 때 삭제할 노드의 바로 앞의 값이나 뒤의 값으로 연결해야 BST의 조건을 위배하지 않는다
바로 앞의 값은 왼쪽 서브 트리에서 가장 큰 값(서브트리에서 계속 오른쪽 서브트리를 탐색했을 때 단말 노드)
바로 다음 값은 오른쪽 서브트리에서 가장 작은 값(서브트리에서 계속 왼쪽 서브트리를 탐색했을 때 단말 노드)
값을 매꾸고 나서는 중복을 허용하지 않기 때문에 이전 위치의 단말 노드는 지워준다
package algorithm;
import java.util.*;
class BinarySearchTree {
Node root;
public static class Node{
int data;
Node left, right;
public Node(int data) {
this.data = data;
}
}
// 탐색
public Node search(Node root, int key) {
// 단말 노드이거나 찾는 노드를 찾았을 때
if(root == null || root.data == key) return root;
// 찾는 값이 더 작을 때 -> 왼쪽 서브 트리 탐색
if(root.data > key) return search(root.left, key);
// 찾는 값이 더 큰 경우 -> 오른쪽 서브 트리 탐색
return search(root.right, key);
}
// 삽입
public void insert(int data) {
root = insert(root, data);
}
private Node insert(Node root, int data) {
// 저장할 위치를 찾았을 때
if(root == null) {
root = new Node(data);
return root;
}
// 저장할 값이 루트 노드보다 작다면 왼쪽 서브 트리로 NULL이 나올 때까지 재귀
if(data < root.data)
root.left = insert(root.left, data);
// 저장할 값이 루트 노드보다 크다면 오른쪽 서브 트리로 NULL이 나올 때까지 재귀
else if(data > root.data)
root.right = insert(root.right, data);
return root;
}
// 삭제
public void delete(int data) {
root = delete(root, data);
}
private Node delete(Node root, int data) {
// 삭제할 노드를 못 찾았을 때
if(root == null) return root;
// 삭제할 데이터가 작으면 왼쪽 서브트리로 이동
if(data < root.data) root.left = delete(root.left, data);
// 삭제할 데이터가 크면 오른쪽 서브트리로 이동
else if(data > root.data) root.right = delete(root.right, data);
// 삭제할 데이터를 찾았을 때
else {
// 삭제할 데이터의 자식 노드가 없을 때
if(root.left == null && root.right == null) return null;
// 삭제할 데이터의 자식 노드가 하나만 있을 때
else if(root.left == null) return root.right;
else if(root.right == null) return root.left;
// 삭제할 데이터의 자식 노드가 두개 있을 때
root.data = findMin(root.right); // 오른쪽 서브 트리에서 가장 작은 값으로 대체
// 대체한 값의 원래 위치에 있는 노드 삭제
root.right = delete(root.right, root.data);
}
return root;
}
// 오른쪽 서브트리에서 가장 작은 값 삭제
int findMin(Node root) {
int min = root.data;
while(root.left != null) {
min = root.left.data;
root = root.left;
}
return min;
}
public void inorder() {
inorder(root);
System.out.println("");
}
private void inorder(Node root) {
if(root != null) {
inorder(root.left);
System.out.print(root.data + " ");
inorder(root.right);
}
}
}
public class BST{
public static void main(String[] args) {
BinarySearchTree tree= new BinarySearchTree();
tree.insert(4);
tree.insert(2);
tree.insert(1);
tree.insert(3);
tree.insert(6);
tree.insert(5);
tree.insert(7);
tree.inorder();
tree.delete(5);
tree.inorder();
}
}
3. 한계점
BST는 삽입, 삭제, 탐색과정에서 모두 트리의 높이만큼 탐색하기 때문에 O(logN)의 시간 복잡도를 가진다
문제는 트리가 편향트리가 되어버렸을 때 결국 배열과 다름 없어지고 시간 복잡도는 O(N)이 된다
'CS > Data Structure' 카테고리의 다른 글
| LRU Cache (0) | 2020.05.22 |
|---|---|
| [자료구조] ProrityQueue(우선순위큐) - Java Collections Framework (0) | 2020.03.23 |
| [자료구조] HashMap(해쉬맵) - Java Collections Framework (0) | 2020.03.23 |

댓글