회귀 분석(Regression Analysis)
관측된 연속형 데이터에 대해 데이터 사이의 관계를 모델링하고 분석하는 기법
1) 회귀 분석 분류
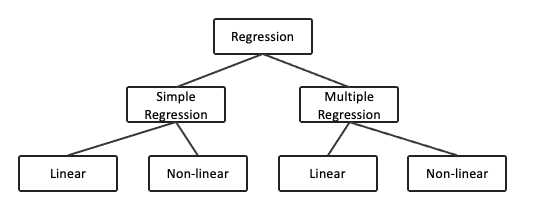
2) 단순 회귀 분석 (단변량 회귀 분석, Simple Regression Analysis)
- 종속 변수를 예측하기 위한 독립 변수가 하나
3) 다중 회귀 분석 (다변량 회귀 분석, Multiple Regression Analysis)
- 종속 변수를 예측하기 위한 독립 변수가 둘 이상
4) 선형 회귀 분석 (Linear Regression Analysis)
- 종속 변수 y와 한 개 이상의 독립 변수(설명 변수) X와의 선형 상관 관계를 모델링하는 분석 기법
- 종속 변수와 하나 이상의 독립변수를 선형으로 가정하고 이를 가장 잘 설명할 수 있는 회귀 계수(Regression Coefficient)를 추정
선형 회귀 분석(Simple Linear Regression Analysis)
1) 단순 선형 회귀 분석 (Simple Liner Regression Analysis)
- 종속변수를 예측하기 위한 독립변수가 하나
- 두 변수 간 선형적인 관계를 가진다는 것을 가정하고 이를 가장 잘 설명할 수 있는 회귀 계수(Regression Coefficient)를 찾아야함
$y = b + Wx $
- 머신러닝의 관점에서 W는 가중치(Weight) 또는 기울기, b는 편향(bias)는 종속변수 y의 절편 으로 표현
$y = \beta_{0} + \beta_{1}x_{1} + \epsilon $
- 통계학 관점에서 상관계수 $ \beta_{0} $ (종속변수의 절편), $ \beta_{1} $ (기울기)와 Noise $ \epsilon $으로 표현
$y_{i} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1} $
- 통계학 관점에서 표본집단을 이용해 모집단의 선형적 관계를 표현할 수 있는 상관계수를 추정
2) 다중 선형 회귀 분석 (Multiple Liner Regression Analysis)
- 종속변수를 예측하기 위한 독립변수가 하나
- 두 변수 간 선형적인 관계를 가진다는 것을 가정하고 이를 가장 잘 설명할 수 있는 회귀 계수(Regression Coefficient)를 찾아야함
$y = b + W_{0}x_{0} + W_{1}x_{1} + ... + W_{n}x_{n} $
- 머신러닝 관점에서 $W_{0}, ... , W_{n} $는 가중치(Weight) 또는 기울기, b는 편향(bias)는 종속변수 y의 절편 으로 표현
$y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + ... + \beta_{n}x_{n} + \epsilon $
- 통계학 관점에서 상관계수 $ \beta_{0} $ (종속변수의 절편), $ \beta_{1}, ... , \beta_{n} $ (기울기)와 Noise $ \epsilon $으로 표현
$y_{i} = \hat{\beta_{0}} + \hat{\beta_{1}}x_{1} + \hat{\beta_{2}}x_{2} + ... + \hat{\beta_{n}}x_{n} $
- 표본집단
3) 회귀 모형에서의 노이즈(Noise)란?
$y = f(x) + \epsilon $
- 데이터 생성 및 수정과정에서 발생할 수 있는 여러 원인들에 의해 발생하는 변동성
4) 최소 자승법 또는 최소 제곱법(OLS, Ordinary Least Squares 또는 LSM, Least Squares Method)
$min( \sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2} )$
- 추정된 회귀식에 의해 결정된 값과 실제값의 오차 제곱항의 차이를 최소화
(1) matrix를 이용한 해 구하기
matrix $ x : n \times (d + 1) $
vector $ y : n \times 1 $
vector $ \hat{\beta} : (d + 1) \times 1 $


matrix x의 1은 상수항을 처리하기위한 요소로 $\beta_{0} $에 해당
$ E(x) = \frac{1}{2}{(y - x\hat{\beta})}^{T} (y - x\hat{\beta}) $
$ \frac{\partial E(x)}{\partial\hat{\beta}} = -x^{T}(y - x\hat{\beta}) = 0 $
$-x^{T}y = x^{T}+x^{T}x\hat{\beta} $
$\hat{\beta} = (x^{T} x)^{-1} x^{T} y $
-> 회귀 계수 $\beta $에 대한 closed form solution을 도출할 수 있음
(2) 최소자승법으로 구한 회귀계수 $\beta $ 가 최적해가 될 수 있는 조건
- 오차항 $ \epsilon $이 정규분포를 따르고 homoskedasticity(동분산성)을 만족
- 종속변수와 독립변수 사이에 선형관계가 성립
- 각 관측치는 서로 독립
'Artificial Intelligence' 카테고리의 다른 글
| RNN, Recurrent Neural Network (0) | 2021.12.12 |
|---|---|
| 선형 회귀 분석(Linear Regression Analysis) (2) (0) | 2021.05.01 |
| [Python] RPA를 위한 웹 자동화 매크로 (0) | 2020.02.04 |
| [Python] 텍스트마이닝 (0) | 2020.02.03 |
| [Python] Regression analysis - Boston (0) | 2020.01.29 |



댓글