문제 >
재현이는 주변을 살펴보던 중 체스판과 말을 이용해서 새로운 게임을 만들기로 했다. 새로운 게임은 크기가 N×N인 체스판에서 진행되고, 사용하는 말의 개수는 K개이다. 말은 원판모양이고, 하나의 말 위에 다른 말을 올릴 수 있다. 체스판의 각 칸은 흰색, 빨간색, 파란색 중 하나로 색칠되어있다.
게임은 체스판 위에 말 K개를 놓고 시작한다. 말은 1번부터 K번까지 번호가 매겨져 있고, 이동 방향도 미리 정해져 있다. 이동 방향은 위, 아래, 왼쪽, 오른쪽 4가지 중 하나이다.
턴 한 번은 1번 말부터 K번 말까지 순서대로 이동시키는 것이다. 한 말이 이동할 때 위에 올려져 있는 말도 함께 이동한다. 말의 이동 방향에 있는 칸에 따라서 말의 이동이 다르며 아래와 같다. 턴이 진행되던 중에 말이 4개 이상 쌓이는 순간 게임이 종료된다.
- A번 말이 이동하려는 칸이
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
- A번 말의 위에 다른 말이 있는 경우에는 A번 말과 위에 있는 모든 말이 이동한다.
- 예를 들어, A, B, C로 쌓여있고, 이동하려는 칸에 D, E가 있는 경우에는 A번 말이 이동한 후에는 D, E, A, B, C가 된다.
- 빨간색인 경우에는 이동한 후에 A번 말과 그 위에 있는 모든 말의 쌓여있는 순서를 반대로 바꾼다.
- A, B, C가 이동하고, 이동하려는 칸에 말이 없는 경우에는 C, B, A가 된다.
- A, D, F, G가 이동하고, 이동하려는 칸에 말이 E, C, B로 있는 경우에는 E, C, B, G, F, D, A가 된다.
- 파란색인 경우에는 A번 말의 이동 방향을 반대로 하고 한 칸 이동한다. 방향을 반대로 한 후에 이동하려는 칸이 파란색인 경우에는 이동하지 않고 방향만 반대로 바꾼다.
- 체스판을 벗어나는 경우에는 파란색과 같은 경우이다.
- 흰색인 경우에는 그 칸으로 이동한다. 이동하려는 칸에 말이 이미 있는 경우에는 가장 위에 A번 말을 올려놓는다.
다음은 크기가 4×4인 체스판 위에 말이 4개 있는 경우이다.
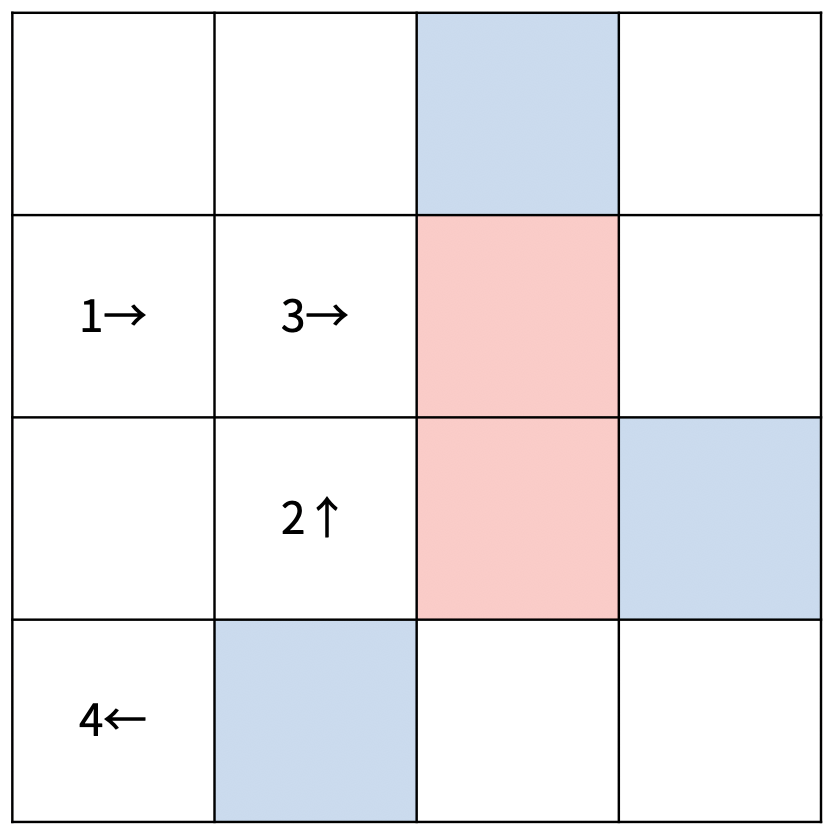
첫 번째 턴은 다음과 같이 진행된다.

두 번째 턴은 다음과 같이 진행된다.
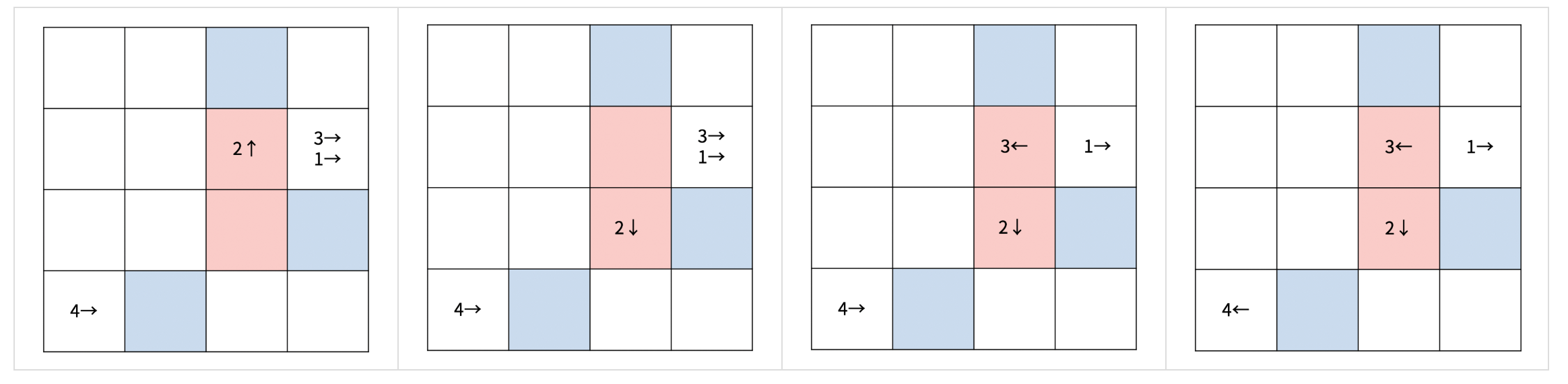
체스판의 크기와 말의 위치, 이동 방향이 모두 주어졌을 때, 게임이 종료되는 턴의 번호를 구해보자.
입력 >
첫째 줄에 체스판의 크기 N, 말의 개수 K가 주어진다. 둘째 줄부터 N개의 줄에 체스판의 정보가 주어진다. 체스판의 정보는 정수로 이루어져 있고, 각 정수는 칸의 색을 의미한다. 0은 흰색, 1은 빨간색, 2는 파란색이다.
다음 K개의 줄에 말의 정보가 1번 말부터 순서대로 주어진다. 말의 정보는 세 개의 정수로 이루어져 있고, 순서대로 행, 열의 번호, 이동 방향이다. 행과 열의 번호는 1부터 시작하고, 이동 방향은 4보다 작거나 같은 자연수이고 1부터 순서대로 →, ←, ↑, ↓의 의미를 갖는다.
같은 칸에 말이 두 개 이상 있는 경우는 입력으로 주어지지 않는다.
출력 >
게임이 종료되는 턴의 번호를 출력한다. 그 값이 1,000보다 크거나 절대로 게임이 종료되지 않는 경우에는 -1을 출력한다.
해결방법 >
시뮬레이션 문제로 고려해야할 점은 말의 좌표와 각 좌표에서 말의 층수, 말의 방향이다.
여기서 층수란, 각 좌표에 여러개의 말이 있을 때, 말이 몇 번째에 쌓여져있는지 나타내는 것이며, 4층이상일 때 게임이 종료되므로
종료조건이 되는 중요한 값이 된다. 따라서 좌표 x, y, 층 수 l, 방향 dx, dy를 변수로 가지는 클래스를 만들고
말이 입력될때마다 객체를 생성한다.
초기 입력 시에 말은 전부 1층인 상태로 입력된다.
다음은 1번 말부터 이동을 시작한다.
말은 이동해야할 칸의 색에 따라 3가지 이동 방법이 있다.
1) 흰색일 경우
a) 현재 말과 좌표가 같으면서 현재말보다 층수가 높은 말이 있는지 탐색한다. 있다면 층수의 오름차순으로 정렬한다.
b) 현재 말이 이동해야할 칸에 말이 존재하는 지 확인하고 존재한다면 제일 높은 층을 찾는다.
c) 현재 말을 이동시키는데 층수는 이동해야할 칸에 말이 있다면 가장 높은 층의 + 1 없다면 1을 값을 저장한다.
d) a)에서 탐색하고 정렬한 말이 n개가 있다면 전부 현재말이 이동한 칸으로 이동시키고 층수는 i번째 말부터
순서대로 현재말의 층수 + i를 저장한다.
2) 빨간색일 경우
a) 현재 말과 좌표가 같으면서 현재말보다 층수가 높은 말이 있는지 탐색한다. 있다면 층수의 내림차순으로 정렬한다.
b) 현재 말이 이동해야할 칸에 말이 존재하는 지 확인하고 존재한다면 제일 높은 층을 찾는다.
c) 현재 말을 이동시키는데 층수는 이동해야할 칸에 말이 있다면 가장 높은 층의 + 1 없다면 1을 값을 저장한다.
d) a)에서 탐색하고 정렬한 말이 n개가 있다면 전부 현재말이 이동한 칸으로 이동시키고 층수는 i번째 말부터
순서대로 현재말의 층수 + i를 저장한다.
3) 파란색일 경우(또는 배열의 범위를 벗어날 경우)
a) 현재 말의 이동방향을 반대로 바꾸고 다시 이동해야할 칸에 대한 이동방법 3가지 중 하나를 선택한다.
b) 만약 파란색에서 3)을 선택하고 또다시 3)을 선택할 경우 그 자리에 그대로 머문다.
[JAVA]
package baekjoon;
import java.util.*;
public class BOJ_17837 {
static int[] dx = {0, 0, -1, 1};
static int[] dy = {1, -1, 0, 0};
static ArrayList <Node> h;
static int win;
static int[][] map;
static int n;
public static class Node implements Comparable<Node>{
int x;
int y;
int dx;
int dy;
int l;
Node(int x, int y, int dx, int dy, int l){
this.x = x;
this.y = y;
this.dx = dx;
this.dy = dy;
this.l = l;
}
@Override
public int compareTo(Node n) {
if(this.l > n.l) return 1;
else return -1;
}
}
public static void blue(Node node, int nx, int ny) {
node.dx *= -1;
node.dy *= -1;
nx = node.x + node.dx;
ny = node.y + node.dy;
if(nx < 0 || ny < 0 || nx >= n || ny >= n || map[nx][ny] == 2) return;
else if(map[nx][ny] == 0) white(node, nx, ny);
else if(map[nx][ny] == 1) red(node, nx, ny);
}
public static void white(Node node, int nx, int ny) {
ArrayList <Node> list = new ArrayList<>();
int top = 0;
list.add(node);
for(int i = 0; i < h.size(); i++) {
if(node.x == h.get(i).x && node.y == h.get(i).y && node.l < h.get(i).l) {
list.add(h.get(i));
}
if(h.get(i).x == nx && h.get(i).y == ny) top = Math.max(top, h.get(i).l);
}
Collections.sort(list);
for(int i = 0; i < list.size(); i++) {
list.get(i).x = nx;
list.get(i).y = ny;
list.get(i).l = top + 1 + i;
if(list.get(i).l >= 4) {
win = 1;
break;
}
}
}
public static void red(Node node, int nx, int ny) {
ArrayList <Node> list = new ArrayList<>();
int top = 0;
list.add(node);
for(int i = 0; i < h.size(); i++) {
if(node.x == h.get(i).x && node.y == h.get(i).y && node.l < h.get(i).l) {
list.add(h.get(i));
}
if(h.get(i).x == nx && h.get(i).y == ny) top = Math.max(top, h.get(i).l);
}
Collections.sort(list, Collections.reverseOrder());
for(int i = 0; i < list.size(); i++) {
list.get(i).x = nx;
list.get(i).y = ny;
list.get(i).l = top + 1 + i;
if(list.get(i).l >= 4) {
win = 1;
break;
}
}
}
public static void go(Node node) {
int nx = node.x + node.dx;
int ny = node.y + node.dy;
if(nx < 0 || ny < 0 || nx >= n || ny >= n || map[nx][ny] == 2) blue(node, nx, ny);
else if(map[nx][ny] == 0) white(node, nx, ny);
else if(map[nx][ny] == 1) red(node, nx, ny);
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int m = sc.nextInt();
map = new int[n][n];
h = new ArrayList<>();
win = 0;
for(int i = 0; i < n; i++) {
for(int j = 0; j < n; j++) {
map[i][j] = sc.nextInt();
}
}
for(int i = 0; i < m; i++) {
int x = sc.nextInt()-1;
int y = sc.nextInt()-1;
int d = sc.nextInt()-1;
h.add(new Node(x, y, dx[d], dy[d], 1));
}
int t = 0;
while(t <= 1000) {
if(win == 1) break;
for(int i = 0; i < h.size(); i++) {
go(h.get(i));
}
t++;
}
if(t == 1001) t = -1;
System.out.println(t);
}
}
'Problem Solving > BOJ' 카테고리의 다른 글
| [백준] 16236번 - 아기 상어 (0) | 2020.03.16 |
|---|---|
| [백준] 15683번 - 감시 (0) | 2020.03.16 |
| [백준] 17140번 - 이차원 배열과 연산 (0) | 2020.03.15 |
| [백준] 15686번 - 치킨 배달 (0) | 2020.03.14 |
| [백준] 17779번 - 게리맨더링 2 (0) | 2020.03.14 |

댓글